倍长中线方法的应用

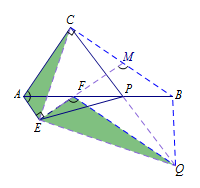
如图，已知$\triangle ABC$是等边三角形，$\triangle BDE$是等腰三角形，且$BD=DE$，$\angle BDE=120^\circ$，取$AE$的中点$F$，连接$DF,CF$．求证：$CF\perp DF$，且$CF=\sqrt 3 DF$．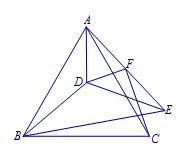

---

分析    结合问题我们把结论转化成证明$\triangle DCQ$为等边三角形或者证明$\triangle DCP$为顶角是$120^\circ$的等腰三角形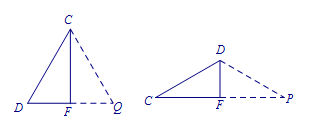．证明    如图，倍长$DF$到$Q$，使$FQ=DF$，则四边形$ADEQ$是平行四边形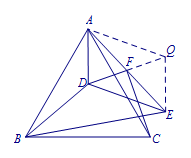．所以

$$AQ=DE=BD,DE\parallel AQ.$$ 所以 $$\angle AGB=\angle GDE=\angle ACB=60^\circ.$$ 所以 $$\angle QAC=\angle DBC.$$ 所以 $$\triangle BDC\cong \triangle AQC.$$ 故$\triangle QCD$为等边三角形，得证．

---

此题倍长中线容易想到，证明三角形全等时夹角相等的证明是难点．其实就是一个“8”字，需要将要证等角的两边延长相交，借助平行线性质来解决．

下面我们给出一道练习
（2015 福建莆田几何压轴题）在$\mathrm{Rt}\triangle ACB$和$\mathrm{Rt}\triangle AEF$中，$\angle ACB=\angle AEF=90^\circ$，将$\triangle AEF$绕着点$A$顺时针旋转，当点$F$落在边$AB$上时，若点$P$是$BF$的中点，连接$PC,PE$，试说明$PC,PE$的数量关系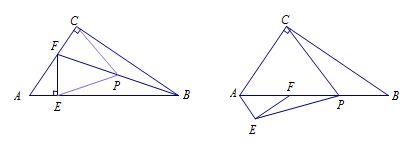．提示