如图，在等边\(\triangle ABC\)中，\(D,E\)分别为\(AB,AC\)的中点，\(M\)为射线\(BC\)上一动点，在\(B\)点异侧作等边\(\triangle DMN\)，判断\(EN\)与\(AB\)的位置关系，并给出证明．
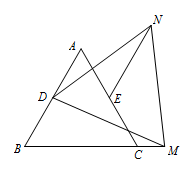
方法一 题中两个等边三角形，线段\(AB\)边上有三个\(60^\circ\)角，由此想到去构造一线三等角模型来证全等．
\(AB\parallel EN\)，证明如下：
如图，延长\(BA\)到\(P\)，使\(PD=BM\)，连接\(PN\)， 则易证\[\triangle PDN \cong \triangle BMD. \] 所以\[\begin{split}\angle P=&\angle B=\angle BAC=60^\circ,\\&PN=BD=AE.\end{split}\] 所以四边形\(AENP\)为平行四边形， 即\(AB\parallel EN\)．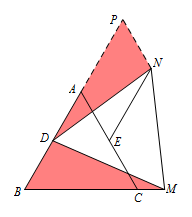 
方法二 若注意到题中\(D,E\)为中点，也可取\(BC\)中点\(F\)构造“手拉手”全等模型．
取\(BC\)中点\(F\)得到等边\(\triangle DEF,\triangle ADE\)，易证\[\triangle EDN \cong \triangle FDM .\]所以\[\angle DEN=\angle DFM=120^\circ.\]从而得到\(AB\parallel EN\)．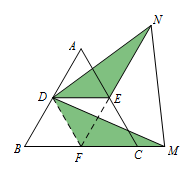 
一道几何题关注的点不一样往往证明的方法就不一样，分析时抓住图形的本质特征、发现几何模型，是作出辅助线的关键．