已知\(O,G,H\)分别为\(\triangle ABC\)的外心、重心和垂心，求证：\(O,G,H\)三点共线，且\(OG=\dfrac 12 GH\)．
本题为著名的欧拉线定理，即：
三角形的外心、重心和垂心在一条直线上，且外心和重心的距离是重心和垂心的距离的一半．
欧拉线定理的证明方法多种多样，今天任性的选择一种不常见的方法来证明．我们都知道欧拉线定理中重要的数量关系是通过三角形相似得到的，所谓不常见的方法不过是证相似的方法不同罢了．
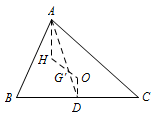
证明 连接\(AH\)，则\(AH\perp BC\)；取\(BC\)中点\(D\)，连接\(OD\)，则\(OD\perp BC\)；连接\(AD,OH\)交于点\(G'\)，则\(\triangle DOG' \sim \triangle AHG'\)．
欲证\(O,G,H\)三点共线，且\(OG=\dfrac 12 GH\)，
只要证明点\(G\)与点\(G'\)重合，\(\triangle DOG'\)与\(\triangle AHG'\)的相似比为\(1:2\)即可．
我们知道三角形的中位线与第三边的比为\(1:2\)，所以构造中位线\(DE\)，得\(\dfrac {DE}{AB}=\dfrac 12\)．
连接\(OE,BH\)，则\(OE \perp AC\)，\(BH \perp AC\)．
由\(AH\parallel DO\)，\(BH\parallel EO\)，\(AB\parallel DE\)，可得\(\triangle AHB \sim \triangle DOE\)，
所以\(\dfrac {OD}{HA}=\dfrac {DE}{AB}=\dfrac 12\)，
则\(\dfrac {DG'}{AG'}=\dfrac {OG'}{HG'}=\dfrac {DO}{AH}=\dfrac 12\)．
由三角形重心的唯一性，可得点\(G'\)即为重心\(G\)，
所以\(O,G,H\)三点共线，且\(OG=\dfrac 12 GH\)．
注 从本题的证明过程中还可以得到：三角形的一个顶点到垂心的距离，是外心到对边距离的\(2\)倍．