如图，矩形\(ABCD\)，\(N\)为平面内一点，连接\(AN,DN\)均与\(BC\)相交，作\(CP\perp AN\)于点\(P\)，\(BQ\perp DN\)于点\(Q\)，两垂线的交点为\(M\)，连接\(MN\)，求证：\(MN\perp AD\)．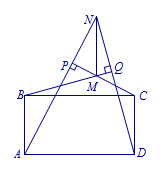
证法一 辅助圆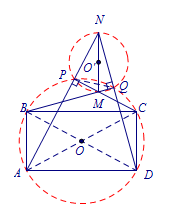
如图，连接\(AC,BD\)交点为\(O\)，则\(A,B,P,Q,C,D\)在以\(O\)为圆心\(OA\)为半径的圆上，同理，取\(MN\)中点\(O'\)，则\(P,M,Q,N\)在以\(O'\)为圆心\(O'M\)为半径的圆上． 所以\[\angle BQP =\angle PNM=\angle BAP,\] 所以\[AB\parallel MN.\] 所以\[MN\perp AD.\]
法二 平移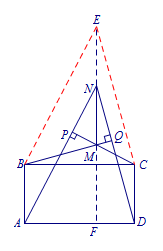
如图，过\(B\)作\(BE\parallel AN\)且\(BE=AN\)，连结\(EN\)，则四边形\(ABEN\)是平行四边形．从而四边形\(ENDC\)也是平行四边形， 由已知，易得\[BQ\perp CE,CP\perp BE，\]则点\(M\)为\(\triangle EBC\)的垂心， 所以\[ME\perp BC.\] 因为\[EN\perp BC,\] 所以\(E,N,M\)三点共线， 故\[MN\perp AD.\]
法三 勾股定理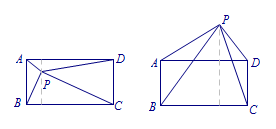
如图，平面内一点\(P\)到矩形四个顶点\(A,B,C,D\)的距离满足\(PA^2+PC^2=PB^2+PD^2\)，所以连接\(BN,CN\)，运用上述结论也可以证明，此种方法运算比较繁琐，不推荐，但是结论需要掌握．