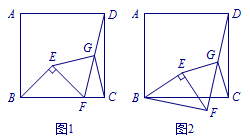
已知正方形\(ABCD\)和等腰\(\mathrm{Rt}\triangle BEF\)，\(BE=EF,\angle BEF=90^\circ\)，按图1放置，使点\(F\)在\(BC\)上，取\(DF\)的中点\(G\)，连接\(EG,CG\)．现将图1中\(\triangle BEF\)绕\(B\)点转动任意角，如图2所示．探究\(EG,CG\)的数量关系和位置关系并证明．
分析 当点\(F\)在\(BC\)上时，不难发现\(EG=CG\)，且\(EG\perp CG\)．现猜想将\(\triangle BEF\)绕\(B\)点转动任意角后，结论仍然成立．
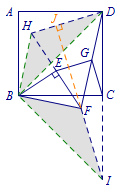
若\(EG=CG\)，\(EG\perp CG\)，则延长\(CG\)至点\(H\)，使得\(GH=GC\)，连接\(EC,EH\)，可得\(\triangle HEC\)为等腰直角三角形．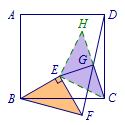
此时构成等腰直角三角形手拉手模型．
连接\(HF\)，有\[\triangle BEC\cong \triangle FEH.\]易得\[HF=BC,\ HF\perp BC.\]即\[HF=CD,\ HF\parallel CD.\]故点\(G\)是\(CH,DF\)的中点．
上述推理过程皆可逆，所以只要将上述过程逆推回去即为证明过程（略）．
从问题的结论出发，追溯导致结论成立的条件，逐步上溯直到使结论成立的条件和已知条件吻合为止，这种逆向思维即是本题所说的“顺瓜摸藤”．
当然，本题从点\(G\)是\(DF\)的中点出发，添加有关的辅助线，也可解决问题．
例如：下图就是基于中点\(G\)构造三角形，使得\(GC,GE\)分别为中位线，从而解决问题．