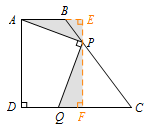
如图，\(AB\perp BC\)，\(AD\parallel BC\)，\(AB=3\)，\(AD=2\)．点\(P\)在线段\(AB\)上，连接\(PD\)，过点\(D\)作\(PD\)的垂线，与\(BC\)相交于点\(C\)．设线段\(AP\)的长为\(m\)，\(\triangle PDC\)的面积为\(S\)，求\(S\)关于\(m\)的函数解析式．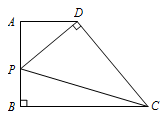
方法一 由\(\angle PAD=\angle PDC=90^\circ\)，可构造“一线三等角”得相似．
如图，过点\(C\)作\(CE\perp AD\)于点\(E\)，则\[\triangle PAD \sim \triangle DEC.\]所以\[\dfrac {AD}{EC}=\dfrac {PD}{DC},\ {即}DC=\dfrac 32PD.\]故\[S_{\triangle PDC}=\dfrac 12PD\cdot DC=\dfrac 34 m^2+3.\]
方法二 图中线段垂直关系较多，可建立平面直角坐标系，用\(m\)表示点\(C\)的坐标，从而由\(S=S_{梯形ABCD}-S_{\triangle PAD}-S_{\triangle PBC}\)得\(S\)关于\(m\)的函数解析式．
如图，\(A(0,3),B(0,0),D(2,3),P(0,3-m)\)．
求得直线\(PD\)解析式为\[y=\dfrac m2 x+3-m.\]由\(CD\perp PD\)可得直线\(CD\)解析式为\[y=-\dfrac 2m x+\dfrac {3m+4}m.\]所以\(C\left(\dfrac {3m+4}2,0\right)\)，则\[\begin{split}S&=S_{梯形ABCD}-S_{\triangle PAD}-S_{\triangle PBC}\\ &=\dfrac 34 m^2+3.\end{split}\]
显然上述两种方法中，代数方法计算量大易出错，几何方法比较简单．一般一条直线上有两个角相等，可考虑添加辅助线构造“一线三等角”模型．
练习 如图，在梯形\(ABCD\)中，\(AB\parallel CD\)，\(AB=2\)，\(AD=4\)，\(\tan C=\dfrac 43\)，\(\angle ADC=\angle DAB=90^\circ\)，\(P\)是腰\(BC\)上一个动点（不含\(B,C\)），作\(PQ\perp AP\)交\(CD\)于点\(Q\)．设\(BP=x\)，\(CQ=y\)，试求\(y\)关于\(x\)的函数解析式．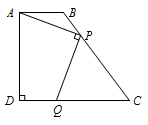
答案 \(y=\dfrac{-5x^2+19x+30}{3x+10}\)．
提示 过点\(P\)作\(CD\)的垂线，交\(AB\)延长线于点\(E\)，交\(CD\)于点\(F\)．