如图,已知\(AD\)为\(\triangle ABC\)的角平分线,\(AB<AC\),在\(AC\)上截取\(CE=AB\),\(M,N\)分别为\(BC,AE\)的中点.求证:\(MN\parallel AD\).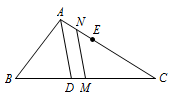
方法一 利用中点构造中位线
连接\(BE\),取\(BE\)中点\(F\),连接\(NF,MF\).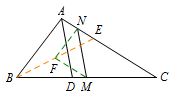 易证\[FM\parallel AC,FN\parallel AB,FM=FN,\]所以\[\angle FNM=\angle FMN=\angle MNC.\]而\(AD\)为\(\triangle ABC\)的角平分线,则\[\angle BAD=\angle DAC=\angle FNM=\angle MNC,\]所以\[MN\parallel AD.\]
易证\[FM\parallel AC,FN\parallel AB,FM=FN,\]所以\[\angle FNM=\angle FMN=\angle MNC.\]而\(AD\)为\(\triangle ABC\)的角平分线,则\[\angle BAD=\angle DAC=\angle FNM=\angle MNC,\]所以\[MN\parallel AD.\]
方法二 利用中点中线倍长
连接\(BN\)并延长至\(F\),使得\(NF=BN\),连接\(CF,EF\).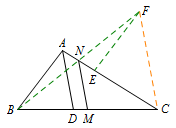 易证\[AB\parallel EF, EF=AB=EC.\]所以\[\angle DAC=\dfrac 12 \angle BAN=\dfrac 12 \angle FEN=\angle ACF.\]则\[AD\parallel CF\parallel MN.\]
易证\[AB\parallel EF, EF=AB=EC.\]所以\[\angle DAC=\dfrac 12 \angle BAN=\dfrac 12 \angle FEN=\angle ACF.\]则\[AD\parallel CF\parallel MN.\]
方法三 利用角平分线将图形翻折
在\(AC\)上截取\(AF=AB\),连接\(BF\)交\(AD\)于点\(G\),则\(BG=FG\).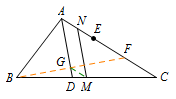 连接\(MG\),易证\[GM\parallel AN,GM=\dfrac 12 FC=AN.\]则四边形\(AGMN\)为平行四边形,所以\[MN\parallel AD.\]
连接\(MG\),易证\[GM\parallel AN,GM=\dfrac 12 FC=AN.\]则四边形\(AGMN\)为平行四边形,所以\[MN\parallel AD.\]
练习 如图,在四边形\(ABCD\)中,\(AB=CD\),\(M,N\)分别为\(AD,BC\)的中点,延长\(BA,CD\),交\(NM\)的延长线分别于点\(E,F\),求证\(\angle BEN=\angle CFN\).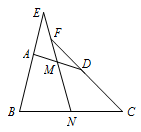 提示
提示
方法一: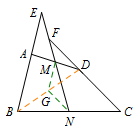
方法二: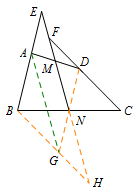
方法三: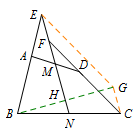

Pingback引用通告: [平面几何]2015年安徽省中考数学压轴题 | 数海拾贝内容系统
Pingback引用通告: 2015年安徽省中考数学压轴题 | Math173