1、在发生某公共卫生事件期间,由专业机构认为该事件在一段事件没有发生在规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”,根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
A.甲地:总体均值为2,总体方差为3
B.乙地:中位数为2,众数为3
C.丙地:总体均值为3,中位数为4
D.丁地:总体均值为1,总体方差大于0
2、已知\(S=\dfrac{\pi}{200000}\cdot\left(\sin\dfrac{\pi}{200000}+\sin\dfrac{2\pi}{200000}+\sin\dfrac{3\pi}{200000}+\cdots+\sin\dfrac{100000\pi}{200000}\right)\),推测下列各值中与\(S\)最接近的是( )
A.\(0.9988\)
B.\(0.9999\)
C.\(1.0001\)
D.\(2.0002\)
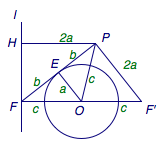
3、过双曲线\(\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0,b>0)\)的左焦点\(F(-c,0)\)作圆\(x^2+y^2=a^2\)的切线,切点为\(E\),延长\(FE\)交抛物线\(y^2=4cx\)于点\(P\),\(O\)为原点,若\(E\)为线段\(FP\)的中点,则双曲线的离心率为_______.
4、当\(a>0\)且\(a\neq 1\)时,函数\(f(x)={\log_a}{(x-1)}+1\)的图象横过点\(A\),若点\(A\)在直线\(mx-y+n=0\)(\(m,n\in\mathcal Z\))上,则\(4^m+2^n\)的最小值为_______.
5、在\(\triangle ABC\)中,角\(A\)、\(B\)、\(C\)所对的边分别为\(a\)、\(b\)、\(c\),且满足\(b^2+c^2-a^2=bc\),\(\overrightarrow{AB}\cdot\overrightarrow{BC}>0\),\(a=\dfrac{\sqrt 3}{2}\),则\(b^2+c^2\)的取值范围是_______.
6、设函数\(f(x)\)在\([a,b]\)上连续,且\(f(a)=f(b)\).证明一定存在长度为\(\dfrac{a-b}{2}\)的区间\([\alpha,\beta]\subset [a,b]\)使得\(f(\alpha)=f(\beta)\).
7、已知函数\(f(x)=\ln x+ax^2+x\).
(1)若\(f(x)\)是\((0,+\infty)\)上的增函数,求\(a\)的取值范围;
(2)已知\(a<0\),对于函数\(f(x)\)图象上任意不同两点\(A(x_1,y_1)\)、\(B(x_2,y_2)\),其中\(x_2>x_1\),直线\(AB\)的斜率为\(k\),记\(N(u,0)\),\(A_1(x_1,0)\),\(B_1(x_2,0)\),若\(\overrightarrow{A_1B_1}=\lambda\overrightarrow{A_1N}(1\leqslant \lambda\leqslant 2)\),求证:\(f'(u)<k\).
参考答案
1、A 2、C
3、\(\dfrac{\sqrt 5+1}{2}\)
提示:如图,\(PF=PH=2a\),利用三角形\(PFH\)与三角形\(FOE\)相似即得.
4、3
5、\(\left(\dfrac 34,\dfrac 54\right)\)
6、提示:构造函数\(F(x)=f\left(x+\dfrac{b-a}2\right)-f(x)\).
7、(1)\([0,+\infty)\);(2)略.
提示:只需要考虑\(N\)为\(A_1B_1\)中点的情形.