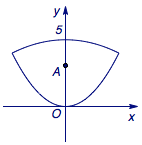
1、已知抛物线\(y=\dfrac 14x^2\)和\(y=-\dfrac 1{16}x^2+5\)所围成的封闭曲线如图所示,给定点\(A(0,a)\),若在此封闭曲线上恰有三对不同的店,满足对每一对点关于点\(A\)对称,则实数\(a\)的取值范围是_______.
2、已知四面体\(ABCD\)的一条棱长为\(x\),其余棱长均为\(1\),记四面体\(ABCD\)的体积为\(F(x)\),则函数\(F(x)\)的单调增区间是_______;最大值为_______.
3、设\(f(x)=\begin{cases}x^3,x<a,\\x&2,x\geqslant a.\end{cases}\)若存在实数\(b\),使得函数\(g(x)=f(x)-b\)有两个零点,则\(a\)的取值范围是_______.
4、设\(n\in\mathcal N^*\),函数\(f(x)=\dfrac{\ln x}{x^n}\),函数\(g(x)=\dfrac{{\mathrm e}^x}{x^n},x\in (0,+\infty)\).
(1)当\(n=1\)时,写出函数\(y=f(x)-1\)的零点个数,并说明理由;
(2)若曲线\(y=f(x)\)与曲线\(y=g(x)\)分别位于直线\(l:y=1\)的两侧,求\(n\)的所有可能取值.
5、设\(F_1\)、\(F_2\)分别为椭圆\(E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)\)的左、右焦点,点\(P\left(1,\dfrac 32\right)\)在椭圆\(E\)上,且点\(P\)和\(F_1\)关于点\(C\left(0,\dfrac 34\right)\)对称.
(1)求椭圆\(E\)的方程;
(2)过右焦点\(F_2\)的直线\(l\)与椭圆相交于\(A\)、\(B\)两点,过\(P\)且平行于\(AB\)的直线与椭圆交于另一点\(Q\),问是否存在直线\(l\),使得四边形\(PABQ\)的对角线互相平分?若存在,求出\(l\)的方程;若不存在,说明理由.
6、已知点列\(T:P_1(x_1,y_1),P_2(x_2,y_2),\cdots,P_k(x_k,y_k)\)(\(k\in\mathcal N^*,k\geqslant 2\))满足\(P_1(1,1)\),且\(\begin{cases}x_i=x_{i-1}+1,\\y_i=y_{i-1}\end{cases}\)与\(\begin{cases}x_i=x_{i-1},\\y_i=y_{i-1}+1\end{cases}\)(\(i=2,3,\cdots,k\))中有且仅有一个成立.
(1)写出满足\(k=4\)且\(P_4(3,2)\)的所有点列;
(2)证明:对于任意给定的\(k(k\in\mathcal N^*,k\geqslant 2)\),不存在点列\(T\),使得\(\sum\limits_{i=1}^k{x_i}+\sum\limits_{i=1}^k{y_i}=2^k\);
(3)当\(k=2n-1\)且\(P_{2n-1}(n,n)(n\in\mathcal N^*,n\geqslant 2)\)时,求\(\sum\limits_{i=1}^k{x_i}\times\sum\limits_{i=1}^k{y_i}\)的最大值.
7、有限数列\(A_n:a_1,a_2,\cdots,a_n(n\geqslant 3)\)同时满足于下列两个条件:
① 对于任意的\(i,j\)(\(1\leqslant i<j\leqslant n\)),\(a_i<a_j\);
② 对于任意的\(i,j,k\)(\(1\leqslant i<j<k\leqslant n\),\(a_ia_j\)、\(a_ja_k\)、\(a_ka_i\)三个数中至少有一个数是数列\(A_n\)中项.
(1)若\(n=4\),且\(a_1=1\),\(a_2=2\),\(a_3=a\),\(a_4=6\),求\(a\)的值;
(2)证明:\(2,3,5\)不可能是数列\(A_n\)中的项;
(3)求\(n\)的最大值.
参考答案
1、D.
2、\(\left(0,\dfrac{\sqrt 6}{2}\right)\).
提示:\(F(x)=\dfrac{1}{12}x\sqrt{3-x^2}\).
3、\(b\in (-\infty,0)\cup (1,+\infty)\).
4、(1)\(0\)个;(2)\(n\in\left\{1,2\right\}\).
5、(1)\(E:\dfrac{x^2}4+\dfrac{y^2}3=1\);(2)\(l:3x-4y-3=0\).
6、(1)(2)略;(3)\(\left[\dfrac 14(n+1)^2(2n-1)^2\right]\).
7、(1)\(a=3\);(2)略;(3)\(n\)的最大值是\(9\).
提示:(3)数列中绝对值大于\(1\)和在\((0,1)\)内的项的个数均至多有\(3\)项,再加上\(-1,0,1\),构造例子为\[A_9:-4,-2,-1,-\dfrac 12,0,\dfrac 14,\dfrac 12,1,2.\]