1.一个平面封闭区域内任意两点距离的最大值称为该区域的“直径”,封闭区域边界曲线的长度与区域直径之比称为区域的“周率”,下面四个平面区域(阴影部分,虚线分别表示正方形、圆、正三角形和圆)的周率从左到右依次记为$\tau_1,\tau_2,\tau_3,\tau_4$,则它们从小到大的排列为_______.
2.已知$x,y,z>0$,且$\dfrac 1x+\dfrac 1y+\dfrac 1z=1$,则$\dfrac x{yz}+\dfrac{y}{zx}+\dfrac{z}{xy}$的最小值是_______.
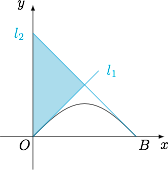
3.直线$l_1,l_2$分别是函数$f(x)=\sin x,x\in [0,\pi]$上$A,B$两点处的切线,且$l_1\perp l_2$.求$l_1,l_2$与$y$轴围成的三角形的面积.
4.等腰三角形的腰长为$a$,一腰上的高为$h$,则以底边为边长的正方形的面积是________.
5.设复数$z$满足$\dfrac{2017z-25}{z-2017}=3+4{\rm i}$,则$|z|=$______.
6.求$3\cos\dfrac{2\pi}5-\cos\dfrac{\pi}5$的值.
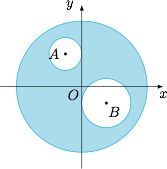
7.如图,一块材质均匀的圆形金属薄片(不计厚度)用圆域$x^2+y^2\leqslant 64$表示,从中挖掉两个小圆洞分别用圆域$(x+2)^2+(y-4)^2\leqslant 4$和$(x-3)^2+(y+2)^2\leqslant 9$表示(圆心依次为$A,B$),则剩下部分的重心的坐标是______.
参考答案
1.$\tau_1,\tau_3,\tau_2,\tau_4$.
容易计算得$\tau_1=2\sqrt 2$,$\tau_2=\pi$,$\tau_3=3$,$\tau_4=2\sqrt 3$.
2.$1$;
由均值不等式,可得\[\sum_{cyc}\dfrac{x}{yz}=\sum_{cyc}\dfrac 12\left(\dfrac{x}{yz}+\dfrac{y}{zx}\right)\geqslant \sum_{cyc}\dfrac 1z=1,\]等号当$x=y=z=3$时取得,于是所求最小值为$1$.
3.$\dfrac 14\pi^2$;
不妨设$A$的横坐标小于$B$的横坐标.由于函数$f(x)$的导函数\[f'(x)=\cos x,\]其值域为$[-1,1]$.于是$A,B$的横坐标分别为$0,\pi$.因此$l_1:y=x$,$l_2:y=-x+\pi$.因此所求的三角形面积为$\dfrac 14\pi^2$.
4.$2a^2\pm a\sqrt{4a^2-h^2}$.
设底边长为$x$,则半周长$p=a+\dfrac x2$,于是由海伦公式得\[\sqrt{\left(a+\dfrac x2\right)\cdot \dfrac x2\cdot \dfrac x2\cdot \left(a-\dfrac x2\right)}=\dfrac 12\cdot a\cdot h,\]即\[x^2\left(4a^2-x^2\right)=4a^2h^2,\]也即\[x^4-4a^2x^2+4a^2h^2=0,\]解得\[x^2=2a^2\pm 2a\sqrt{a^2-h^2}.\]
另法 设等腰三角形顶角为$\theta$,则有$\sin\theta=\dfrac ha$,从而有$$S=\left(2a\sin\dfrac{\theta}2\right)^2=2a^2\left(1-\cos\theta\right)=2a^2\left(1\pm\dfrac{\sqrt{a^2-h^2}}{a}\right).$$
5.$5$.
设$x=3+4{\rm i}$,则有\[2017z-25=xz-2017x,\]于是\[z=\dfrac{25-2017x}{2017-x},\]从而\[z\cdot \overline z=\dfrac{(25-2017x)(25-2017\overline x)}{(2017-x)(2017-\overline x)}=\dfrac{25^2-2017\cdot 25(x+\overline x)+2017^2\cdot 25}{2017^2-2017(x+\overline x)+25}=25,\]因此$|z|=5$.
注 事实上,我们有\[z=\dfrac{\overline x-2017}{2017-x}\cdot x,\]于是$|z|=|x|=5$.
6.$\dfrac{-2+\sqrt 5}2$;
由\[\cos\dfrac{\pi}5+\cos\dfrac{3\pi}5+\cos\dfrac{5\pi}5+\cos\dfrac{7\pi}5+\cos\dfrac{9\pi}5=0,\]可得\[\cos\dfrac{\pi}5-\cos\dfrac{2\pi}5=\dfrac 12.\]又\[\cos\dfrac{\pi}5\cdot\cos\dfrac{2\pi}5=\dfrac{\sin\dfrac{\pi}5\cos\dfrac{\pi}5\cos\dfrac{2\pi}5}{\sin\dfrac{\pi}5}=\dfrac 14.\]于是\[\begin{split}3\cos\dfrac{2\pi}5-\cos\dfrac{\pi}5&=-2\left(\cos\dfrac{\pi}5-\cos\dfrac{2\pi}5\right)+\left(\cos\dfrac{\pi}5+\cos\dfrac{2\pi}5\right)\\
&=-1+\sqrt{\left(\dfrac 12\right)^2+4\cdot \dfrac 14}\\
&=\dfrac{-2+\sqrt 5}2.\end{split}\]
7.$\left(-\dfrac{19}{51},\dfrac 2{51}\right)$.
相当于圆心为$O(0,0)$,重量为$64$的金属片上覆盖了圆心为$A(-2,4)$,重量为$-4$的金属片以及圆心为$B(3,-2)$,重量为$-9$的金属片,其重心坐标为\[G\left(\dfrac{64\cdot 0-4\cdot (-2)-9\cdot 3}{64-4-9},\dfrac{64\cdot 0-4\cdot 4-9\cdot (-2)}{64-4-9}\right),\]即$G\left(-\dfrac{19}{51},\dfrac 2{51}\right)$.
注 此即定比分点坐标公式\[\left(\dfrac{x_1+\lambda x_2}{1+\lambda},\dfrac{y_1+\lambda y_2}{1+\lambda}\right)\]的升级版,也是重心坐标公式\[\left(\dfrac{x_1+x_2+x_3}{3},\dfrac{y_1+y_2+y_3}3\right)\]的加权版.