练习题集[84]基础练习

1．设函数$f(x)=ax^2+bx+c$($a,b,c\in\mathcal R$且$a>0$)．记$p$：$f(x)$与$f(f(x))$均恰好有两个零点，$q$：$f\left(f\left(-\dfrac b{2a}\right)\right)<0$，则$p$是$q$的_______条件．

2．已知定义在$(0,+\infty)$上的函数$f(x)$满足对任意$x>0$，均有$f'(x)<2xf(x)+{\rm e}^{x^2}$，其中$f'(x)$是函数$f(x)$的导函数．若$f(1)={\rm e}$，则不等式$f(x)\geqslant x{\rm e}^{x^2}$的解集是_______．

3．如图放置的边长为$1$的正方形$PABC$沿$x$轴滚动．设顶点$P(x,y)$的轨迹方程是$y=f(x)$，则函数$f(x)$的最小正周期为_______；$y=f(x)$在其两个相邻的零点间的图象与$x$轴所围成区域的面积为_______．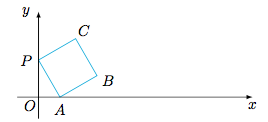

4．在四面体$ABCD$中，$AB=CD$，$AC=BD$，$AD=BC$，下列判断错误的是（　　）
A．该四面体的三组对棱的中点连线两两垂直
B．该四面体的外接球球心与内切球球心重合
C．该四面体的各面是全等的锐角三角形
D．该四面体中任意三个面两两所成的二面角的正弦值之和为$1$

5．设函数$f(x)=ax^3+3bx$($a<0,b>0$)，当$x\in [0,1]$时，有$f(x)\in [0,1]$，则$b$的最大值是_______．

6．如图，直角$\triangle ABC$与直角$\triangle DEF$全等，$\angle BAC=30^\circ$，$AB=4$，$O$为$AB,DE$的中点，直线$CF$与$DA$交于点$H$，则$BH$的最小值为________．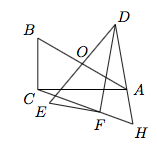

7．设函数$f(x)=ax^2+(2b+1)x-a-2$($a,b\in\mathcal R$，$a\neq 0$)．
(1) 若$a=-2$，求函数$y=|f(x)|$在$[0,1]$上的最大值$M(b)$；
(2) 若函数$f(x)$在区间$(0,1)$有两个不同的零点，求证：$\dfrac{(2+a)(1-2b)}{a^2}<\dfrac{1}{16}$．

 

---

参考答案

1．充分必要．

提示　函数$f(f(x))$有两个零点等价于函数$f(x)$的两个零点$x_1,x_2$($x_1<x_2$)满足$x_1<\min f(x)<x_2$，即$x_1<f\left(-\dfrac b{2a}\right)<x_2$．

2．$(0,1]$．

提示　函数$F(x)=\dfrac{f(x)}{{\rm e}^{x^2}}-x$的导函数$F'(x)<0$．

3．$4$，$\pi+1$．

根据题意可以作出一个周期内的函数图象，如图．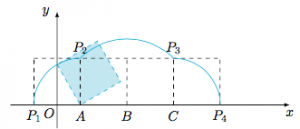

4．D．

提示　在长方体中研究四面体$ABCD$，使四面体的$6$条棱均为长方体的面对角线．选项A,C容易证明其正确性；对于选项B，考虑到四面体的外接球球心即长方体的中心，而四面体的各个面全等，因此长方体的中心到四个面的距离相等，进而可知命题正确；对于选项D，正四面体$ABCD$即为反例．

5．$\dfrac{\sqrt 3}2$．

提示　$f(x)$的零点为$x=0$和$x=\sqrt{\dfrac{3b}{-a}}$，极大值点为$x=\sqrt{\dfrac{b}{-a}}$，极大值为$2b\sqrt{\dfrac{b}{-a}}$．
按极大值点$\sqrt {-\dfrac ba}$与$1$的大小关系进行分类讨论：
若$\sqrt {-\dfrac ba}\geqslant 1$，即$a+b\geqslant 0$时，有$f(1)=a+3b\leqslant 1$，此时$b\leqslant \dfrac 12$；
若$\sqrt {-\dfrac ba}<1$，即$a<-b$时，有$2b\sqrt{\dfrac {b}{-a}}\leqslant 1$且$f(1)=a+3b\geqslant 0$，整理得$a\leqslant -4b^{3}$且$a\geqslant -3b$，从而有$-3b\leqslant -4b^3$，又$b>0$，解得$b\leqslant \dfrac {\sqrt 3}{2}$．当$a=-\dfrac 32\sqrt 3$，$b=\dfrac{\sqrt 3}{2}$时取到等号．

6．作点 $O$ 关于 $AC$ 的对称点 $G$，连接 $OC,OF$，如图．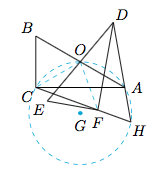
由已知可得$\triangle BOC$与$\triangle EOF$全等，于是 $$\angle BOC+\angle COE=\angle EOF+\angle COE=\angle DOA,$$ 进而$\triangle CFO$与$\triangle ADO$全等，$\angle OCF=\angle DAB$，从而$C,O,A,H$ 四点共圆．设外接圆半径为 $r$，由正弦定理得 $$\dfrac{OC}{\sin \angle BAC}=2r,$$ 所以$r=2$，因为 $OG=CG=AG=AO=2$，所以动点 $H$ 在以 $G$ 为圆心，$2$ 为半径的圆上，因此当 $B,H,G$ 三点共线，且点 $H$ 位于点 $B,G$ 中间时 $BH$ 最小，且 $$BH=BG-r=2\sqrt 3-2.$$

7．(1) $a=-2$时， $$f(x)=-2x^2+(2b+1)x=-2x\left(x-b-\dfrac 12\right).$$ 所以$y=|f(x)|$的最值可能在$0,1,\dfrac b2+\dfrac 14$处取到，先分别计算 $$f(0)=0,f(1)=2b-1,f\left(\dfrac b2+\dfrac 14\right)=\dfrac {(2b+1)^2}{8}\geqslant 0.$$ 当$\dfrac b2+\dfrac 14<0$或$\dfrac b2+\dfrac 14>1$，即$b<-\dfrac 12$或$b>\dfrac 32$时， $$M(b)=|f(1)|=|1-2b|;$$ 当$-\dfrac 12\leqslant b\leqslant \dfrac 32$时，有 $$M(b)=\max\left\{|f(1)|,f\left(\dfrac b2+\dfrac 14\right)\right\}.$$ 当$-\dfrac 12\leqslant b\leqslant \dfrac 12$时，考虑到 $$f\left(\dfrac b2+\dfrac 14\right)-|f(1)|=\dfrac {4b^2+20b-7}{2},$$ 所以当$b<\dfrac {4\sqrt 2-5}{2}$时，$f\left(\dfrac b2+\dfrac 14\right)<|f(1)|$，此时$M(b)=|f(1)|$；
当$\dfrac {4\sqrt 2-5}{2}\leqslant b\leqslant \dfrac 12$时， $$M(b)=f\left(\dfrac b2+\dfrac 14\right).$$ 当$\dfrac 12<b\leqslant \dfrac 32$时，$f\left(\dfrac b2+\dfrac 14\right)>f(1)=|f(1)|$，所以$M(b)=f\left(\dfrac b2+\dfrac 14\right)$；
综上有，
$$M(b)=\begin{cases} 1-2b,&b<\dfrac{4\sqrt 2-5}2,\\ \dfrac 18(1+2b)^2,&\dfrac{-5+4\sqrt 2}2\leqslant b\leqslant \dfrac 32,\\ 2b-1,&b>\dfrac 32.\end{cases}$$

(2) 一方面，有$f(0)\cdot f(1)=(-a-2)(2b-1)$．另一方面，设$f(x)$的两个零点分别为$x_1,x_2$，则$f(x)=a(x-x_1)(x-x_2)$，于是 $$\begin{split} f(0)\cdot f(1)=&a(-x_1)(-x_2)\cdot a(1-x_1)(1-x_2)\\=&ax_1(1-x_1)x_2(1-x_2)\\\leqslant &a^2\cdot\left(\dfrac {x_1+1-x_1}{2}\right)^2\cdot\left(\dfrac {x_2+1-x_2}{2}\right)^2\\=&\dfrac{a^2}{16},\end{split}$$ 因为$x_1\ne x_2$，所以等号取不到，于是原命题得证．