练习题[14]创新能力培养基础练习

1、过抛物线\(x^2=2py\)（\(p>0\)）的焦点作斜率为\(1\)的直线与该抛物线交于\(A\)、\(B\)两点，\(A\)、\(B\)在\(x\)轴上的正投影分别为\(D\)、\(C\)，若梯形\(ABCD\)的面积为\(12\sqrt 2\)，则\(p=\)_______．

 2、方程\(ay=b^2x^2+c\)中的\(a,b,c\in\left\{-3,-2,0,1,2,3\right\}\)，且\(a,b,c\)互不相同，在所有这些方程表示的曲线中，不同的抛物线共有_______条．

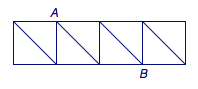
3、沿图中的线段移动，且在移动的过程中不允许经过重复的点或线段，则从\(A\)点到\(B\)点共有_______种不同的移动方法．

4、已知函数\(f(x)=3x+a\)和\(g(x)=3x+2a\)的零点都在区间\((b,c)\)内，则\[\dfrac{a^2+2ab+2ac+4bc}{b^2-2bc+c^2}\]的最小值为_______．

5、抛物线的弦与过弦的端点的两条切线所围成的三角形称为阿基米德三角形．阿基米德三角形有一些有趣的性质，如：若弦过焦点，那么其所对的顶点在准线上．那么此时的阿基米德三角形面积的最小值为_______．（设抛物线的焦点与准线的距离为\(p\)）

6、在平面直角坐标系\(xOy\)中，如果菱形\(OABC\)的边长为\(2\)，点\(B\)在\(y\)轴上，则菱形内（不包括边界）的整点（横坐标和纵坐标都是整数的点）个数的取值集合是_______．

7、若函数\(f(x)\)满足：集合\(A=\left\{f(n)\left|n\in\mathcal N^*\right.\right\}\)中至少存在三个不同的数构成等比数列，则称函数\(f(x)\)是等比源函数．

（1）判断下列函数：

① \(y=x^2\)；

② \(y=\dfrac 1x\)；

③ \(y={\log_2}x\)

中，哪些是等比源函数？（不需证明）

（2）判断函数\(f(x)=2^x+1\)是否为等比源函数，并证明你的结论；

（3）证明：对于任意的\(d,b\in\mathcal N^*\)，函数\(g(x)=dx+b\)都是等比源函数．

---

参考答案

1、\(2\)

2、\(62\)

3、\(25\)

4、\(-1\)      提示：注意到\[\dfrac{a^2+2ab+2ac+4bc}{b^2-2bc+c^2}+1=\dfrac{\left(a+b+c\right)^2}{\left(b-c\right)^2}.\]

5、\(p^2\)．

6、\(\left\{0,1,3,4\right\}\)．

7、（1）均为等比源函数；（2）不是；（3）略．

提示：（3）注意二项式定理\[\left(1+b\right)^n=1+b\left({\mathrm C}_n^1+{\mathrm C}_n^2b+\cdots+{\mathrm C}_n^nb^{n-1}\right).\]