1、已知正整数$x,y$满足$x^2+82x+2013=y^2$,则$x+y=$( )
A.$123$
B.$124$
C.$125$
D.$126$
2、数列$\{a_n\}$中,已知$a_1=20$,$a_2=13$,$a_3=31$,$a_4=18$,且当$n\geqslant 5$时,$a_n=a_{n-1}-a_{n-2}+a_{n-3}-a_{n-4}$,则数列的前$2014$项和是( )
A.$64$
B.$82$
C.$62$
D.$42$
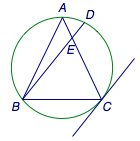
3、三角形$ABC$内接于圆$O$,且$AB=AC$,过点$B$作圆$O$在顶点$C$处切线的平行线交圆于另外一点$D$,$AC$、$BD$交于点$E$,$AB=8$,$BC=6$,则$AE=$( )
A.$4$
B.$3$
C.$\dfrac 72$
D.$\dfrac 52$
4、将包含甲、乙两队的$8$支队伍平分成$2$个小组参加某项比赛,则甲、乙两队被分在两个不同的小组的方案种数为( )
A.$20$
B.$35$
C.$40$
D.$60$
5、设$\omega$为方程$x^3=1$的虚根,则$(1-\omega+\omega^2)\cdot (1+\omega-\omega^2)$的值为( )
A.$4$
B.$\omega$
C.$\omega^2$
D.$1$
6、椭圆$\dfrac{x^2}{9}+\dfrac{y^2}{4}=1$的右焦点为$F$,$P_1,P_2,\cdots,P_{24}$为椭圆上$24$个逆时针方向排列的点,其中$P_1$是椭圆的右顶点,且$$\angle P_1FP_2=\angle P_2FP_3=\cdots=\angle P_{23}FP_{24}=\angle P_{24}FP_1,$$则这$24$个点到椭圆右准线的距离的倒数之和为( )
A.$2\sqrt 5$
B.$6\sqrt 5$
C.$2\sqrt 3$
D.$6\sqrt 3$
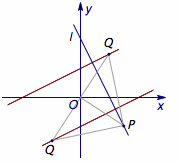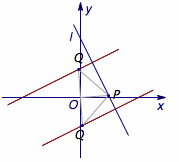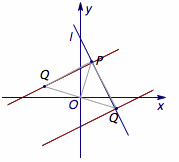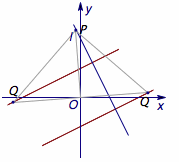
7、在平面直角坐标系$xOy$中,点$P$、$Q$分别为直线$l:2x+y-3=0$与圆$M:(x-2)^2+y^2=r^2$($r>0$)上的动点.若$P$、$O$、$Q$可以构成等腰直角三角形,则$r$的最小值为( )
A.$\dfrac{\sqrt{10}}{10}$
B.$\dfrac{\sqrt 5}5$
C.$\dfrac{3\sqrt {10}}{10}$
D.以上答案均不正确
参考答案
1、C 提示 配方可得$$(x+41)^2+332=y^2,$$移项,应用平方差公式因式分解得$$(y-x-41)\cdot (y+x+41)=2^2\cdot 83,$$由于等式左边的两个因数同奇偶,于是只可能为$2\cdot 166$,因此$$y+x+41=166,$$即$$x+y=125.$$
2、B 提示 数列以$10$为周期,且前$10$项为:$$20,13,31,18,-20,-20,-13,-31,-18,20,$$因此$S_{2014}=S_4=82$.
3、C 提示 三角形$ABC$与三角形$BEC$相似.
4、A 提示 $\dfrac 12{\rm C}_8^4-{\rm C}_6^2=20$.
5、A 提示 $\omega^2+\omega+1=0$.
6、B 提示 由椭圆的第二定义可得点$P_i$到右准线的距离的倒数为$e\cdot\dfrac{1}{P_iF}$,其中$e$为椭圆的离心率,$i=1,2,\cdots,24$.
对于椭圆,我们有常用结论:椭圆的焦点弦被焦点所分的两条线段的调和平均数为半通径长$\dfrac{b^2}{a}$.
于是应用该结论,有$$\sum_{i=1}^{24}\left(e\cdot\dfrac{1}{P_iH}\right)=\dfrac{\sqrt 5}3\cdot\left(\dfrac{a}{b^2}\cdot 24\right)=6\sqrt 5.$$
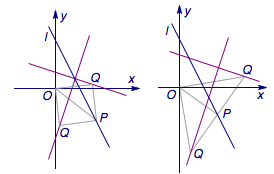
7、D 提示 考虑当$P$运动时,$Q$点所有可能的位置形成的轨迹,因为直角顶点不确定,所以需要讨论.
当\(O\)为直角顶点时,\(Q\)点的轨迹为两条直线,如图.
同理,当\(Q\)或\(P\)为直角顶点时,轨迹分别是两条直线,如图:
六条直线方程分别为$x-2y+3=0$,$x-2y-3=0$,$3x-y-3=0$,$x+3y-3=0$,$x+3y-6=0$,$3x-y-6=0$.因此$r$的最小值为圆心$M(2,0)$到六条直线距离的最小者,而圆心恰好在其中一条直线上,所以$r$的最小值不存在.