2013年全国高中数学联赛四川省预赛第10题:
关于曲线\(C:x^4+y^2=1\)的下列命题:
① 曲线\(C\)关于原点对称;
② 曲线\(C\)关于直线\(y=x\)对称;
③ 曲线\(C\)所围成的面积小于\(\pi\);
④ 曲线\(C\)所围成的面积大于\(\pi\).
其中的真命题是_______.(写出所有真命题的编号)
正确答案是 ①④.
解 先考虑对称性,再比较面积.
① 由于对曲线\(C\)上任意一点\((x,y)\)均有\[(-x)^4+(-y)^2=x^4+y^2,\]于是曲线关于原点对称;
② 由于并不是对曲线\(C\)上任意一点\((x,y)\)均有\[y^4+x^2=1,\]如\(\left(\left(\dfrac 12\right)^{1/4},\left(\dfrac 12\right)^{1/2}\right)\),于是曲线并不关于直线\(y=x\)对称;
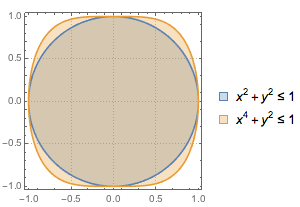
③④ 问题即比较曲线\(C\)与圆\(x^2+y^2=1\)围成的区域面积.由于两者均分布在\[-1\leqslant y\leqslant 1\]的区域内,且当\(y=\pm 1\)时,两条曲线对应的横坐标的值均为\(0\),因此可以利用祖暅原理将平面区域的面积比较问题转化为纵坐标一致的截线段长度的比较问题.
事实上,任何一条平行于\(x\)轴的直线\[y=m,-1<m<1\]被两条曲线截得的线段长分别为\(2\sqrt [4]{1-m^2}\)(曲线\(C\))以及\(2\sqrt {1-m^2}\)(圆),而前者任何时候都大于后者(因为小于\(1\)的整数的算术平方根比自身大),因此根据祖暅原理的推论可得曲线\(C\)所围成的面积大于圆所围成的面积\(\pi\),如图.