每日一题[16] 抛物线的光学性质

本题是2015年北京市东城区高二期末考试的选择最后一题改成的填空题．题干简洁干净，考察点也同样清晰明朗；难度方面，思路入口宽，但想要真正解出并不容易．总的来说就是小巧的试题，深厚的背景，是道难得的好题．

 点$P$到点$A\left(\dfrac 12,0\right),B(a,2)$及到直线$x=-\dfrac 12$的距离都相等，如果这样的点恰好只有一个，那么$a$的值是________．

---

正确答案是$\pm\dfrac 12$．

注意到$P$点在以$A$为焦点，直线$x=-\dfrac 12$为准线的抛物线$E:y^2=2x$上．因此可设$P\left(2t^2,2t\right)$，于是由$P$到焦点$A$与到点$B$的距离相等，得

$$2t^2+\dfrac 12=\sqrt{(2t^2-a)^2+(2t-2)^2},$$ 整理得 $$(2-4a)t^2-8t+a^2+\dfrac{15}4=0.$$ 该方程的解集有且只有一个元素，因此 $$2-4a=0\lor\begin{cases}2-4a\neq 0\\\Delta=0,\end{cases}$$ 即 $$a=\dfrac 12\lor a=-\dfrac 12.$$

这一解法思路简单，也有可行性，但其中涉及到解一个三次方程，运算量不低．另外，解法平淡无奇，没有美感．有没有漂亮的解法呢？

我们知道，解析几何是几何的一个分支，因此解析几何试题应当从几何的层面找寻本源．$P$到$A$与$P$到$B$的距离相等，于是问题可以转化为线段$AB$的垂直平分线$l$与抛物线只有一个公共点，这包含两种情形．

 第一种情形，$l$与抛物线的对称轴平行．此时

$$l:y=1,$$ 于是 $$a=\dfrac 12.$$

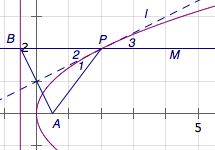
第二种情形，$l$与抛物线相切．如图，过$P$作射线$PM\parallel x$轴．根据抛物线的几何性质，$\angle 1=\angle 3$，因此$\angle 1=\angle 2=\angle 3$，于是$PB\parallel x$轴．因此$P$点坐标为$(2,2)$，进而

$$PB=PA=2+\dfrac 12,$$ 解得 $$a=-\dfrac 12.$$

综合以上两种情形，我们就得到了答案．