已知点\(A(-1,1)\)，若曲线\(G\)上存在两点\(B,C\)，使得三角形\(ABC\)为正三角形，则称\(G\)为\(T\)型曲线．给定下列三条曲线：
① \(y=-x+3(0\leqslant x\leqslant 3)\)；
② \(y=\sqrt{2-x^2}(-\sqrt{2}\leqslant x\leqslant 0)\)；
③ \(y=-\dfrac{1}{x}(x>0)\)．
则其中是\(T\)型曲线的为________．
正确答案是 ③．
解 判定一个三角形为正三角形有很多种方式：三边相等的三角形；有一个角为\(60^\circ\)的等腰三角形；底边上的高与底边比值为\(\dfrac{\sqrt 3}{2}\)的等腰三角形等．在动态问题中讨论正三角形的存在性问题时，通过利用顶角为\(60^\circ\)的三角形为正三角形进行判定．
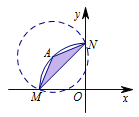
对于①，如图，曲线\(G\)为线段\(MN\)，以\(A\)为圆心作圆与\(G\)交于两点构成等腰三角形．
由于顶点的最大值小于\(60^\circ\)，从而不存在满足要求的\(B,C\)两点；
对于②，如图，曲线\(G\)为一段圆弧，以\(A\)为圆心作圆与\(G\)交于两点构成等腰三角形．
由于顶角的最小值大于\(60^\circ\)，从而不存在满足要求的\(B,C\)两点；
对于③，如图，曲线\(G\)为反比例曲线在第四象限的部分，以\(A\)为圆心作圆与\(G\)交于两点构成等腰三角形．
由于顶角\(\angle BAC\)的范围为\(0^\circ<\angle BAC<90^\circ\)，且连续变化，所以存在满足条件的\(B,C\)两点．
注一 在判断运动中是否存在某个特殊状态时，往往需要找到刻画状态的量，如在本题中构造等腰三角形后顶角的大小就可以刻画状态是否符合要求，这种量称为运动的“特征量”．此时可以由运动的连续性得到特征量变化的连续性，从而可以根据连续介值定理对特征量可能的取值加以判断．因此特征量的构造与对特征量取值可能的论证是解决这类问题的两个核心步骤．
注二 “特征量”有时也称为“不变量”，更多的例题可以参考 每日一题[15]不变量与“完美点”．
下面给出一道练习．
曲线\(C:y=\dfrac 1x(x>0)\)上是否存在两点\(M,N\)，使得\(\triangle OMN\)为等腰直角三角形？
提示 本题涉及到如何确定一个等腰直角三角形，我们在曲线\(C\)上任取一点\(M\)，将\(OM\)逆时针旋转\(45^\circ\)与\(C\)相交得到点\(N\)，取\(\dfrac{OM}{ON}\)为特征量，考查当\(M\)在曲线上移动时这个量的可能取值，如图．
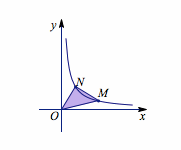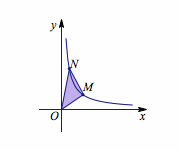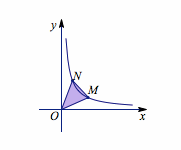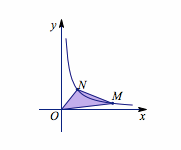当\(\dfrac{OM}{ON}\)的值为\(\sqrt{2}\)或\(\dfrac{\sqrt 2}{2}\)时，\(\triangle OMN\)为等腰直角三角形．结合图象可知，存在符合题意的两点\(M,N\)．