每日一题[229] “L-距离”

2014年高考福建卷文科数学第12题（原题为选择压轴题，有改动）：

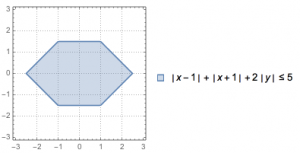
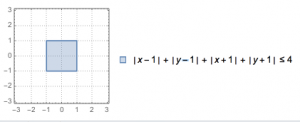
在平面直角坐标系中，两点\(P_1(x_1,y_1)\)，\(P_2(x_2,y_2)\)间的“L-距离”定义为\(||P_1P_2||=\left|x_1-x_2\right|+\left|y_1-y_2\right|\)，求平面内与\(x\)轴上两个不同的定点\(F_1,F_2\)的“L-距离”之和等于定值（大于\(||F_1F_2||\)）的点的轨迹形状．

正确的答案如图．

可以看到，题中轨迹的定义与椭圆的定义相仿，得到的图形也与椭圆神似，我们可以称之为“L-椭圆”．那么是否有“L-圆”，“L-双曲线”，“L-抛物线”等等其他“L-”图形呢？

答案是肯定的．

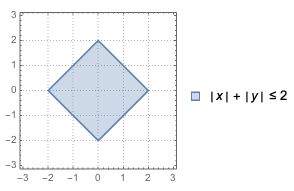
“L-圆”：平面内到定点的“L-距离”为定值的点的轨迹．

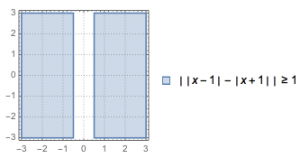
“L-双曲线”：平面内到两个定点的“L-距离”之差的绝对值为定值（小于\(||F_1F_2||\)）的点的轨迹．

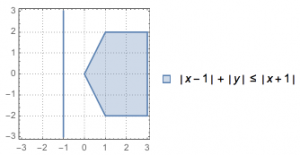
“L-抛物线”：平面内到定点的“L-距离”与到定直线的“L-距离”（即到直线上的点的“L-距离”的最小值）相等的点的轨迹．

其实类似的还有

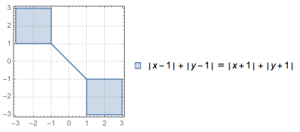
“L-线段”：平面内到两个定点的“L-距离”之和为两个定点之间的“L-距离”的点的轨迹．

“L-垂直平分线“：平面内到两个定点的“L-距离”相等的点的轨迹．

看了这么多“L-图形”，是不是觉得很有趣呢？