每日一题[228] 横看成岭侧成峰

已知三角形\(ABC\)的外接圆圆心为\(O\)，且\(3\overrightarrow {OA}+4\overrightarrow{OB}+5\overrightarrow {OC}=\overrightarrow 0\)，则角\(C\)等于_______．

正确答案是\(\dfrac{\pi}4\)．

解    从不同的角度看待问题，可以得到不同的解决方案．

法一    注意到\(\angle C=\dfrac 12\angle AOB\)，因此直接以\(O\)为起点求解．

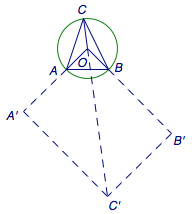
如图，分别延长\(OA\)、\(OB\)和\(CO\)至\(A'\)、\(B'\)、\(C'\)，使得\(\overrightarrow{OA'}=3\overrightarrow{OA}\)，\(\overrightarrow{OB'}=4\overrightarrow{OB}\)，\(\overrightarrow{OC'}=5\overrightarrow{CO}\)．

根据题意，有\[\overrightarrow{OC'}=\overrightarrow{OA'}+\overrightarrow{OB'},\]于是四边形\(OA'C'B'\)为平行四边形，且\(OA'=3\)，\(OB'=4\)，\(OC'=5\)．

显然\(OA'C'B'\)为矩形，\(\angle A'OB'=\dfrac{\pi}2\)，进而\(C=\dfrac{\pi}4\)．

法二    考虑到条件基于\(O\)点，而待求量基于\(C\)点，因此考虑转化起点．

利用向量的换底公式\[\overrightarrow{AB}=\overrightarrow{MB}-\overrightarrow{MA}\]将条件的起点换为\(C\)：\[3\left(\overrightarrow {CA}-\overrightarrow{CO}\right)+4\left(\overrightarrow{CB}-\overrightarrow{CO}\right)-5\overrightarrow{CO}=\overrightarrow 0,\]整理得\[\overrightarrow{CO}=\dfrac 14\overrightarrow{CA}+\dfrac 13\overrightarrow{CB},\]两边分别与\(\overrightarrow {CA}\)与\(\overrightarrow{CB}\)作数量积，得\[\begin{cases}\dfrac 12b^2=\dfrac 14b^2+\dfrac 13ab\cos C,\\\dfrac 12a^2=\dfrac 14ab\cos C+\dfrac 13a^2,\end{cases}\]于是可得\[\cos C=\dfrac{3b}{4a}=\dfrac{2a}{3b},\]进而求得\(\cos C=\dfrac{\sqrt 2}2\)，\(C=\dfrac{\pi}{4}\)．

法三    考虑到外接圆的特性，有\[\overrightarrow{OA}\cdot\overrightarrow{OA}=\overrightarrow{OB}\cdot\overrightarrow{OB}=\overrightarrow{OC}\cdot\overrightarrow{OC}.\]

不妨设设外接圆的半径为\(1\)．已知条件两边分别与\(\overrightarrow{OA}\)、\(\overrightarrow{OB}\)、\(\overrightarrow{OC}\)作数量积，有\[\begin{cases}\overrightarrow {OA}\cdot \left(3\overrightarrow{OA}+4\overrightarrow{OB}+5\overrightarrow {OC}\right)=\overrightarrow{OA}\cdot\overrightarrow 0,\\ \overrightarrow {OB}\cdot \left(3\overrightarrow{OA}+4\overrightarrow{OB}+5\overrightarrow {OC}\right)=\overrightarrow{OB}\cdot\overrightarrow 0,\\ \overrightarrow {OC}\cdot \left(3\overrightarrow{OA}+4\overrightarrow{OB}+5\overrightarrow {OC}\right)=\overrightarrow{OC}\cdot\overrightarrow 0,\end{cases}\]化简得\[\begin{cases} 4\cos\angle AOB+5\cos\angle AOC=-3,\\ 3\cos\angle  AOB+5\cos\angle BOC=-4,\\3\cos\angle AOC+4\cos\angle BOC=-5.\end{cases}\]解得\[\begin{cases}\cos\angle AOB=0,\\ \cos\angle BOC=-\dfrac{4}{5},\\ \cos\angle AOC=-\dfrac{3}{5},\end{cases}\]所以\(\angle AOB=\dfrac{\pi}2\)，故\( C=\dfrac{\pi}4\)．