每日一题[222] 函数的“分解”

2015年高考重庆卷理科数学第16题：

若函数$f(x)=|x+1|+2|x-a|$的最小值为$5$，则实数$a=$_______.

---

正确答案为$-6\lor 4$．

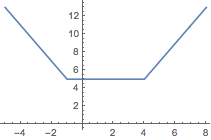
解    先回顾一个我们较为熟悉的函数$g(x)=|x+1|+|x-a|$，其函数值的几何意义为数轴上表示$x$的点到表示$-1$和$a$的点的距离之和，函数图象以$x=\dfrac{-1+a}2$为对称轴，如图所示．

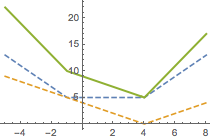
接下来思考，如果这个函数再加上另一个函数$h(x)=|x-a|$，对函数的图象会造成什么样的影响？

如图，函数$h(x)$的加入会使得函数图象在$x=a$处“下沉”（图中$a>-1$，但并不影响本质），于是函数$f(x)$在$x=a$处取得最小值，所求$a$的值可以由

$$|a+1|=5$$ 解得．

当然，也可以采用如下的代数描述：

根据已知，有

$$\begin{split}f(x)&\geqslant \left|(x+1)-(x-a)\right|+|x-a|\\&=|1+a|+|x-a|\\&\geqslant |1+a|,\end{split}$$ 等号当$x=a$时取得．以下略．

下面给出一道练习题．

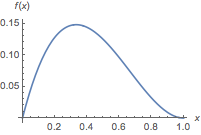
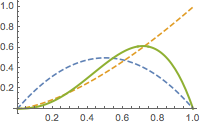
（2011年·安徽·理10）函数$f(x)=ax^m(1-x)^n$在区间$[0,1]$上的图象如图所示，则$m,n$的值可能是（        ）

A. $m=1,n=1$

B. $m=1,n=2$

C. $m=2,n=1$

D. $m=3,n=1$

答案为B．

解    将$f(x)$分解为两个函数的乘积：

$$f(x)=ax^n(1-x)^n\cdot x^{m-n},$$ 前一个部分的图象关于$x=0.5$对称．

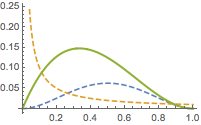
当$m<n$时，函数$y=x^{m-n}$的图象在$x=0.5$两侧为左高右低，因此会引起函数图象的“重心”向左侧移动，如图．

当$m=n$时，函数$f(x)$的图象关于$x=0.5$对称，不符合题意；

当$m>n$时，函数$y=x^{m-n}$的图象在$x=0.5$两侧为左低右高，因此会引起函数图象的“重心”向右侧移动，如图．