2025年高考全国II卷 #14
一个底面半径为 $4~{\rm cm}$,高为 $ 9 ~{\rm cm}$ 的封闭圆柱形容器(容器壁厚度忽略不计)内有两个半径相等的铁球,则铁球半径的最大值为 _____${\rm cm}$.
答案 $\dfrac 52$.
解析 当两个铁球外切且与圆柱形容器的侧面以及上下底面均相切时半径最大,如图为圆柱的轴截面 $ABCD$,$AB=8$,$BC=9$,铁球球心分别为 $O_1,O_2$,设 $O_1$ 在 $AB,AD$ 上的投影分别为 $E,F$,$O_2$ 在 $O_1F$ 上的投影为 $G$.
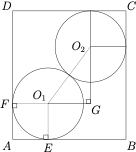
设铁球的半径为 $r$,则在直角三角形 $O_1GO_2$ 中,有\[|O_1O_2|^2=|O_1G|^2+|O_2G|^2\implies (2r)^2=(8-2r)^2+(9-2r)^2\iff (2r-5)(2r-29)=0,\]于是所求铁球半径的最大值 $r=\dfrac 52$.
