已知函数 $f(x)=\begin{cases} x^2-2 x, &x \geqslant a, \\ 2^x+a, &x<a .\end{cases}$ 给出下面四个结论:
① 当 $a=1$ 时 $f(x)$ 只有一个零点;
② 对任意 $a>3$,$f(x)$ 既没有最大值,也没有最小值;
③ 存在实数 $ a $,$f(x)$ 在 $ \mathbb{R} $ 上单调递增;
④ 若 $ f(x)$ 存在最小值,则 $ a $ 的最小值为 $ -1$.
其中所有正确结论的序号是_____.
答案 ①②④.
解析 函数 $f_1(x)=2^x+a$($x<a$)的图象是从 $A(-\infty,a)$ 到 $B(a,2^a+a)$ 的递增开曲线;函数 $f_2(x)=x^2-2x$($x\geqslant a$)的图象是从 $C(a,a^2-2a)$ 到 $D(+\infty,+\infty)$ 的左闭右开曲线.
分析零点 讨论分界点为 $2^a+a=0$ 的实数解 $a=a_1$ $^{[1]}$,以及 $a=0,2$,有\[\begin{array}{c|c|c|c|c|c|c|c}\hline\ a&(-\infty,a_1)&a_1&(a_1,0)&0&(0,2)&2&(2,+\infty) \\ \hline f_1(x)~\text{的零点个数}&0&0&1&0&0&0&0\\ \hline f_2(x)~\text{的零点个数}&2&2&2&1&1&1&0\\ \hline \end{array}\] 因此 $f(x)$ 的零点个数为\[\begin{cases} 0,&a\in (2,+\infty),\\ 1,&a\in[0,2],\\ 2,&a\in(-\infty,a_1],\\ 3,&a\in(a_1,0).\end{cases}\]
分析单调性 讨论分界点为 $a=1$. 当 $a<1$ 时,$f(x)$ 在 $(-\infty,a)$ 上单调递增,在 $[a,1]$ 上单调递减,在 $[1,+\infty)$ 上单调递增; 当 $a\geqslant 1$ 时,$f(x)$ 在 $(-\infty,a)$ 上单调递增,在 $[a,+\infty)$ 上单调递增.但由于 $f(a^-)>f(a)$,于是 $f(x)$ 并不在 $\mathbb R$ 上单调递增.
分析最值 当 $x\to +\infty$ 时,有 $f(x)\to +\infty$,因此函数 $f(x)$ 没有最大值.关于最小值,讨论分界点为 $a=-1,1$ 以及 $a=a^2-2a$ 的实数解 $a=0,3$,
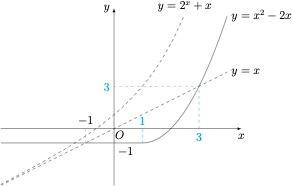
当 $a<-1$ 时,$f(x)$ 没有最小值,有下确界 $a$; 当 $-1\leqslant a\leqslant 1$ 时,$f(x)$ 有最小值 $-1$; 当 $1<a\leqslant 3$ 时,$f(x)$ 有最小值 $a^2-2a$; 当 $a>3$ 时,$f(x)$ 没有最小值,有下确界 $a$.
根据以上分析,所有正确结论的序号为 ①②④.
