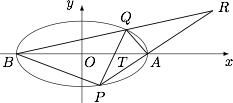
已知$A,B$是椭圆$\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$的长轴顶点，$P,Q$是椭圆上的两点，且满足$k_{AP}=\lambda k_{QB}$($\lambda>1$)．
(1) 求证：直线$AP$和$BQ$的交点在定直线上；
(2) 求证：直线$PQ$过定点；
(3) 求$\triangle PQB$和$\triangle PQA$面积之差的最大值．
分析与解 (1) 根据题意，有\[\begin{split} AP&:y=k_{AP}(x-a),\\ BQ&:y=k_{QB}(x+a),\end{split}\]于是直线$AP$与$BQ$的交点横坐标$x_0$满足\[\dfrac{x_0+a}{x_0-a}=\lambda,\]于是\[x_0=\dfrac{\lambda+1}{\lambda-1}\cdot a.\]因此直线$AP$与$BQ$的交点在定直线$x=\dfrac{\lambda+1}{\lambda-1}\cdot a$上．
(2) 由椭圆的垂径定理，有\[k_{AQ}\cdot k_{BQ}=-\dfrac{b^2}{a^2},\]于是\[k_{AP}\cdot k_{AQ}=-\dfrac{b^2}{a^2}\cdot \lambda.\]将坐标系原点平移至$A(a,0)$，则椭圆方程为\[\dfrac{(x'+a)^2}{a^2}+\dfrac{y'^2}{b^2}=1,\]与直线$P'Q'$的方程$mx'+ny'=1$化齐次联立可得\[\dfrac{x'^2}{a^2}+\dfrac {2x'}a\cdot (mx'+ny')+\dfrac{y'^2}{b^2}=0,\]也即\[\dfrac{1}{b^2}y'^2+\dfrac{2n}{a}x'y'+\left(\dfrac{2m}a+\dfrac{1}{a^2}\right)x'^2=0,\]因此\[b^2\cdot \left(\dfrac{2m}a+\dfrac{1}{a^2}\right)=-\dfrac{b^2}{a^2}\cdot \lambda,\]解得\[m=-\dfrac{1+\lambda}{2a}.\]于是直线$P'Q'$恒过点$T'\left(-\dfrac{2a}{1+\lambda},0\right)$，也即原坐标系下的$T\left(\dfrac{\lambda-1}{\lambda+1}\cdot a,0\right)$．
(3) 因为$|BT|-|AT|=2|OT|$，根据题意得到，所求面积之差为$\triangle OPQ$面积的$2$倍．利用伸缩变换\[\begin{cases} x'=x,\\y'=\dfrac abx,\end{cases} \]将椭圆变为圆$x'^2+y'^2=a^2$，此时点$T'$的坐标不变，为$\left(\dfrac {\lambda-1}{\lambda+1}\cdot a,0\right)$，三角形$OP'Q'$面积的两倍等于$$2\cdot\dfrac 12\cdot a^2\sin\angle P'OQ'=a^2\sin\angle P'OQ'.$$考虑过定点$T'$的弦所对的圆心角即可，于是得到其最大值为\[\begin{cases}ab,&\dfrac{\lambda-1}{\lambda+1}\geqslant \dfrac{\sqrt 2}2,\\2ab\cdot \dfrac{\lambda-1}{\lambda+1}\cdot \sqrt{1-\left(\dfrac{\lambda-1}{\lambda+1}\right)^2},&\dfrac{\lambda-1}{\lambda+1}<\dfrac{\sqrt 2}2,\end{cases}\]也即\[\begin{cases}ab,&\lambda\geqslant 3+2\sqrt 2,\\4ab\cdot \dfrac{\sqrt{\lambda}\cdot (\lambda -1)}{(\lambda+1)^2},&1<\lambda<3+2\sqrt 2.\end{cases}\]
注 本题来自尬题29．