平面上有两条线段$AB=3$,$AC=5$,且$\angle BAC=\dfrac{\pi}6$,则线段$AB$和$AC$在该平面上任意一条直线$l$上的投影的长度之和的取值范围是_________.
正确答案是$\left[\dfrac 32,\sqrt{34+15\sqrt 3}\right]$.
分析与解 设投影直线的方向向量为$\overrightarrow n$,记$\langle \overrightarrow n,\overrightarrow {AB}\rangle =x$,注意到$\cos(-x)=\cos x$,所以投影长度之和一定可以写成\[m=\left|3\cos x\right|+\left|5\cos\left(x+\dfrac{\pi}6\right)\right|.\]设\[\begin{split}f(x)&=\left|3\cos x+5\cos\left(x+\dfrac{\pi}6\right)\right|,\\g(x)&=\left|3\cos x-5\cos\left(x+\dfrac{\pi}6\right)\right|,\end{split}\]则\[m=\max\{f(x),g(x)\}.\]
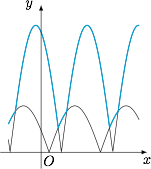
如图,作出函数$f(x)$与$g(x)$的图象.
$m$的最大值即为函数$f(x)$的最大值\[\sqrt{\left(3+\dfrac{5\sqrt 3}2\right)^2+\left(-\dfrac 52\right)^2}=\sqrt{34+15\sqrt 3}.\]$m$的最小值当\[3\cos x+5\cos\left(x+\dfrac{\pi}6\right)=3\cos x-5\cos\left(x+\dfrac{\pi}6\right)\]时,也即$x=\dfrac{\pi}3$取得,此时$m=\dfrac 32$.
综上所述,所求投影的长度之和的取值范围是$\left[\dfrac 32,\sqrt{34+15\sqrt 3}\right]$.
注 本题来自尬题18,类似问题见每日一题[709]向量问题的两个角度.