已知棱长为$2$的正方体$ABCD-A_1B_1C_1D_1$的中心为$O$，$P$是正方体表面上一点，且直线$OP$与直线$AB_1$所成的角为$\dfrac{\pi}4$，求$OP$的取值范围．
正确答案是$\left[1,\dfrac 32\right]$．
分析与解 法一 如图，设$M,N,U,V$分别为$B_1C_1,AD,A_1D_1,BC$的中点，则$P$点的轨迹是以$MN$为轴，$O$点为母线与轴的公共点，$\alpha=\dfrac{\pi}4$的圆锥面被正方体的表面截得的截线．根据对称性，只需要考虑平面$A_1C_1$与平面$CD_1$截圆锥面形成的截线．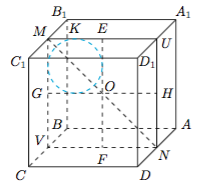 
显然$EF,GH$是圆锥面的两条母线，作与$EF,GH,MU$均相切的圆，设该圆与$MU$相切于$K$．考虑圆锥面的轴$MN$与平面$A_1C_1$形成的线面角大小$\beta_1=\dfrac{\pi}4$，于是平面$A_1C_1$上的截线为抛物线$ST$，且以$K$为焦点，以底面$A_1C_1$的中心$E$为顶点．容易求得$S,T$为边$C_1D_1,B_1A_1$的靠近点$C_1,B_1$的四等分点．
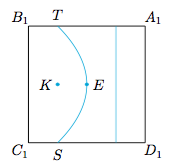类似的，由于圆锥面的轴$MN$与平面$C_1D$形成的线面角大小$\beta_2=0$，于是平面$C_1D$上的截线为离心率等于$\sqrt 2$的双曲线．显然双曲线与棱的公共点亦为抛物线与棱的公共点，不难得知所求的取值范围即$\left[OE,OS\right]$，即$\left[1,\dfrac 32\right]$．
注 平面截圆锥面所成的圆锥曲线（也可能为圆）的类型与该平面与圆锥的轴的夹角$\beta$，以及圆锥的母线与轴的夹角$\alpha $的大小关系相关，得到的圆锥曲线的离心率$e=\dfrac {\cos\beta}{\cos\alpha}$．
法二 建系求解
以$C$为坐标原点$CD,CB,CC_1$为$x,y,z$轴建立空间直角坐标系．则$O(1,1,1)$，$\overrightarrow {AB_1}=(-2,0,2)$，由对称性知，只需要分别考虑点$P$在平面$A_1B_1C_1D_1$与平面$CDD_1C_1$上即可：
若点$P$在平面$A_1B_1C_1D_1$上，设$P(x,y,2)$，则$\overrightarrow {OP}=(x-1,y-1,1)$，有$$\cos\dfrac{\pi}4=\dfrac {\sqrt 2}{2}=\dfrac {|-2(x-1)+2|}{\sqrt{4+0+4}\cdot\sqrt {(x-1)^2+(y-1)^2+1}},$$化简得$(y-1)^2=2(1-x)$，由$x\in[0,2],y\in[0,2]$进一步得到$x\in\left[\dfrac 12,1\right]$，从而有$$OP^2=(x-1)^2+(y-1)^2+1=(x-1)^2+2(1-x)+1=(x-2)^2\in\left[1,\dfrac 94\right],$$从而此时$OP\in\left[1,\dfrac 32\right]$．
当点$P$在平面$CDD_1C_1$上时，设$P(x,0,z)$，同理可得坐标满足的关系为$$(x-1)(z-1)=-\dfrac 12,$$由范围限制知$|x-1|\in\left[\dfrac 12,1\right ]$，设$m=|x-1|$，有$$OP^2=(x-1)^2+(z-1)^2+1=m^2+\dfrac 1{4m^2}+1\in\left[2,\dfrac 94\right],$$于是有此时$OP\in\left[\sqrt 2,\dfrac 32\right]$．
综上知，$OP\in\left[1,\dfrac 32\right]$．