在直角$\triangle ABC$中，$B$为直角，$A=60^\circ$，$AB=4\sqrt 3$，点$D$在$BC$边上，且$BD=2$，点$G$在$AB$边上，点$E,F$在$AC$边上，线段$DE$与$GF$相交于点$O$．若$DE=GF$且$\angle EOF=60^\circ$，求四边形$DGEF$面积的取值范围．
答案 $\left[\dfrac{25\sqrt 3}4,\dfrac{31\sqrt 3}3\right]$．
分析与解 根据题意，$CD=10$，设$\angle DEC=\theta$，在$\triangle CDE$中，由正弦定理得$$DE=\dfrac{5}{\sin\theta}.$$又因为$\angle EOF=\angle A$，所以$\angle AGF=\theta$，于是$$\dfrac{AF}{\sin\theta}=\dfrac{GF}{\sin 60^\circ}=\dfrac{DE}{\sin 60^\circ},$$于是$AF=\dfrac{10}{\sqrt 3}$，点$F$是$AC$边上的一个定点，如图：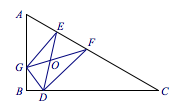
当点$G$在边$AB$上运动时，$$\sin\theta=\sin\angle AGF\in[\sin\angle ABF,1],$$由余弦定理解得$\sin\angle ABF=\dfrac 52\sqrt{\dfrac 3{31}}$，于是$$DE=\dfrac {5}{\sin\theta}\in\left[5,2\sqrt{\dfrac{31}3}\right].$$所以四边形$DGEF$的面积$$S=\dfrac 12DE^2\cdot \sin 60^\circ=\dfrac {\sqrt 3}4DE^2,$$于是其取值范围是$\left[\dfrac{25\sqrt 3}4,\dfrac{31\sqrt 3}3\right]$．