每日一题[546]远近高低各不同

已知函数$f(x)=\dfrac{2(1-a)+\cos x}{a-\sin^2x}$的值域包含区间$[1,2]$，求$a$的取值范围．

---

分析    函数$f(x)$即

$$f(x)=\dfrac{\cos x+2(1-a)}{\cos^2x-(1-a)},$$ 于是先解决问题以下问题：

已知函数$y=\dfrac{x+2a}{x^2-a}$($x\in[-1,1]$且$x^2\neq a$)的值域包含$[1,2]$，求$a$的取值范围．

考虑先从值域包含$y=1$和$y=2$入手得到必要条件缩小讨论范围，然后再论证充分性．

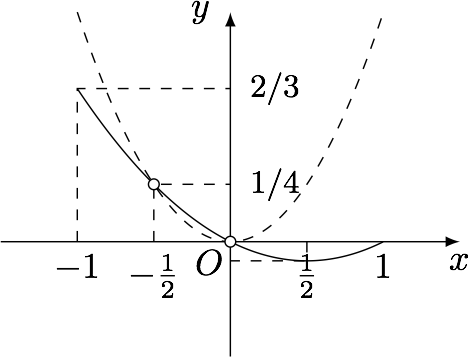
解    若值域包含$y=1$，则

$$\begin{cases} x^2-a=x+2a,\\x^2-a\neq 0,\end{cases}$$ 即 $$\begin{cases} a=\dfrac 13x^2-\dfrac 13x,\\ a\neq x^2,\end{cases}$$ 如图．

可得$a\in\left[-\dfrac{1}{12},\dfrac 14\right)\cup\left(\dfrac 14,\dfrac 23\right]$．

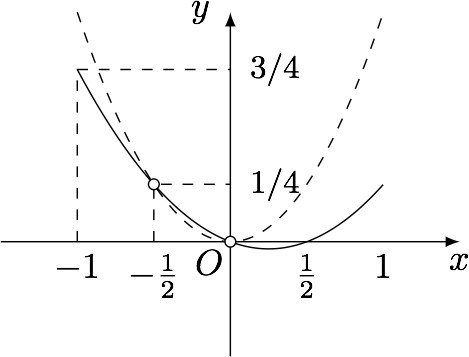
若值域包含$y=2$，则

$$\begin{cases} 2x^2-2a=x+2a,\\ x^2-a\neq 0,\end{cases}$$ 即 $$\begin{cases} a=\dfrac 12x^2-\dfrac 14x,\\ a\neq x^2,\end{cases}$$ 如图．

可得$a\in\left[-\dfrac 1{32},\dfrac 34\right]$．

这样，我们就得到了$a\in\left[-\dfrac{1}{32},\dfrac 14\right)\cup\left(\dfrac 14,\dfrac 23\right]$．接下来论证充分性．

第一种情形，$-\dfrac 1{32}\leqslant a<0$时，函数连续，因此其值域必然包含$[1,2]$，符合题意．

第二种情形，$a=0$时，函数为$y=\dfrac 1x$，因此其值域包含$[1,2]$，符合题意．

第三种情形，$0<a<\dfrac 14$时，由于

$$-\sqrt a<-2a<\sqrt a,$$ 于是函数在区间$(-\sqrt a,\sqrt a)$上可以取得全体实数（函数在此区间上连续，考虑两边的单边极限即可得到），符合题意．

第四种情形，$\dfrac 14<a\leqslant \dfrac 23$时，函数在$[-1,-\sqrt a)$上单调递增趋于无穷大，而

$$f(-1)=\dfrac{2a-1}{1-a}\leqslant 1,$$ 因此其值域包含$[1,2]$，符合题意．

综上所述，$a$的取值范围是$\left[-\dfrac{1}{32},\dfrac 14\right)\cup\left(\dfrac 14,\dfrac 23\right]$．

回到原问题，$a$的取值范围是$\left[\dfrac 13,\dfrac 34\right)\cup\left(\dfrac 34,\dfrac {33}{32}\right]$．

---

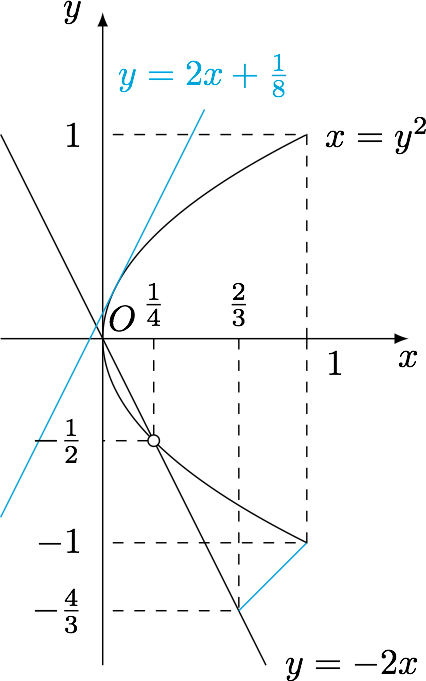
另法    函数$y=\dfrac{x+2a}{x^2-a}$可以看成是抛物线$x=y^2$($-1\leqslant y\leqslant 1$)的点与直线$y=-2x$上的点连线的斜率，如图．