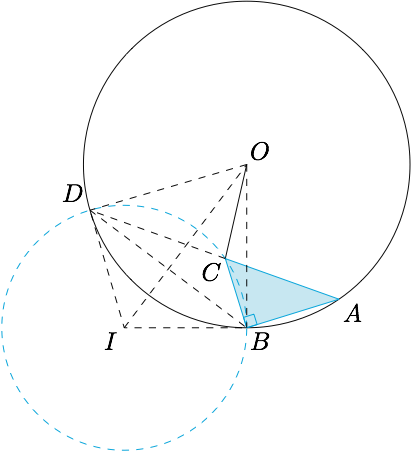
如图,圆$O$的半径为$r$,直角三角形$ABC$的顶点$A,B$在圆$O$上,$\angle B$为直角,$\angle A$的大小为$\theta$,$C$在圆内部(包括边界).当点$A$在圆$O$上运动时,$OC$的最小值为_______.
分析 延长$AC$交圆$O$于$D$,则由于$\angle A$的大小为定值,于是$D$为定点,且$\angle DCB=\dfrac{\pi}2+\theta$为定值,所以$C$的轨迹是圆弧.
解 设$C$点的轨迹所在的圆圆心为$I$,半径为$r'$,则由于$$\dfrac 12BD=r\sin \theta,\dfrac 12\angle BID=\pi -\angle BCD=\dfrac{\pi}2-\theta,$$因此$$r'=r\tan\theta,$$而$$OI=r\cos\theta+r'\cos\left(\dfrac{\pi}2-\theta\right)=r\cos\theta+r'\sin\theta,$$于是$OC$的最小值为$$r\cos\theta+r'\sin\theta-r'=\dfrac{1-\sin\theta}{\cos\theta}\cdot r.$$