每日一题[448]发现定向量

边长为$2$的正三角形$ABC$（包括边界）内有点$P$，$\overrightarrow{PB}\cdot\overrightarrow{PC}=1$，则$\overrightarrow{AP}\cdot\overrightarrow{AB}$的取值范围是_______．

---

正确答案是$\left[\dfrac{3-\sqrt 5}2,3-\sqrt 5\right]$．

分析与解    $\overrightarrow{PB}$与$\overrightarrow{PC}$的差$\overrightarrow{CB}$为定向量，因此可以利用极化恒等式

$$4\overrightarrow{PB}\cdot\overrightarrow{PC}=\left(\overrightarrow{PB}+\overrightarrow{PC}\right)^2-\left(\overrightarrow{PB}-\overrightarrow{PC}\right)^2$$ 化简得 $$\overrightarrow{PB}\cdot\overrightarrow{PC}=PM^2-\dfrac 14BC^2,$$ 其中$M$为边$BC$的中点，进而$PM^2=2$．这样我们就得到了$P$的轨迹是以$M$为圆心，$\sqrt 2$为半径的圆在三角形内部（包括边界）的部分．

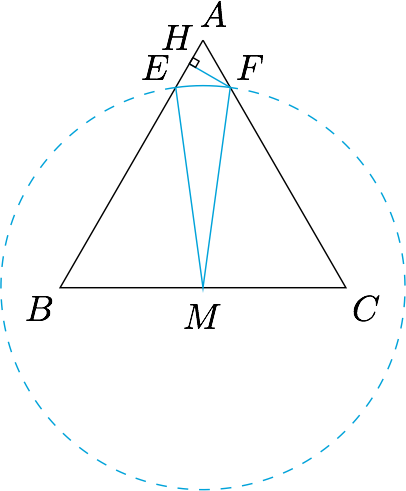
接下来，考虑到$\overrightarrow{AB}$为定向量，因此只需要计算$\overrightarrow{AP}$在$\overrightarrow{AB}$方向上的投影数量的取值范围．如图，在$\triangle BME$中应用余弦定理可得

$$EM^2=BE^2+BM^2-2\cdot BE\cdot BM\cdot \cos B,$$ 从而 $$BE=\dfrac{1+\sqrt 5}2,$$ 于是 $$AE=2-BE=\dfrac{3-\sqrt 5}2.$$ 而 $$AH=\dfrac 12AF=\dfrac 12AE=\dfrac{3-\sqrt 5}4.$$ 注意$\angle HFM$为钝角，因此所求的数量积的取值范围是$\left[\dfrac{3-\sqrt 5}2,3-\sqrt 5\right]$．