每日一题[438]变化中的不变量

这是一个老师与我交流的题目改编而来的趣题：

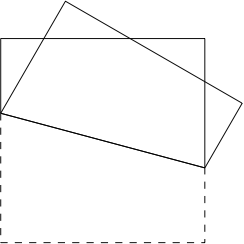
将边长为$1$的正方形纸片沿经过其中心的直线对折，求对折后的纸片所能覆盖的最大面积．

正确答案是$2-\sqrt 2$．

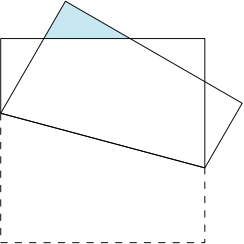
解    注意到对折后纸片所覆盖的面积为正方形面积的一半，再加上图示的小三角形面积的两倍．

经过观察可以发现，在不同的对折方案中，图中小三角形的周长始终为定值，为正方形的边长（想一想，为什么？）．设$a,b,c$为小三角形的三边长，其中$c$为斜边长，则有 $$a+b+c=1,a^2+b^2=c^2,$$ 消去$c$得 $$\dfrac 12=a+b-ab\geqslant 2\sqrt {ab}-ab,$$ 从而 $$\sqrt{ab}\leqslant \dfrac{2-\sqrt 2}2,$$ 因此小三角形面积的最大值为 $$\dfrac 12\left(\dfrac{2-\sqrt 2}2\right)^2=\dfrac{3-2\sqrt 2}4,$$ 当$a=b=1-\dfrac{\sqrt 2}2$，$c=\sqrt 2-1$时取得．因此所求的最大值为$2-\sqrt 2$．

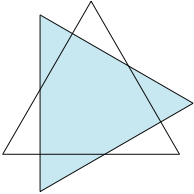
作为练习，可以把纸片换为边长为$1$的正三角形，答案为$\dfrac{\sqrt 3}{6}$．

提示    将对折后的纸片沿对折时使用的直线作对称可以得到所求面积的两倍为正三角形纸片的面积再加上三个小三角形的面积，如图．