每日一题[402]最大张角问题

这是我在“数海拾贝读者俱乐部”看到的题：

在$\triangle ABC$中，角$A$是钝角，$AB=3$，$\overrightarrow {BC}\cdot\overrightarrow {BA}=12$，当角$C$最大时，$\triangle ABC$的面积等于____．

---

正确答案是$3$．

解　记角$A,B,C$所对的边长为$a,b,c$，由题意知

$$c=3,a\cos B=4.$$ 所以点$C$在如下图的直线$l$上（也可以直接通过向量的数量积得到向量$\overrightarrow {BC}$在向量$\overrightarrow {BA}$上的射影长为$4$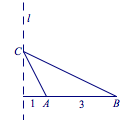）：问题转化成当点$C$在直线$l$上运动时，角$C$何时有最大值？

考虑过点$A,B$的圆，当圆与直线$l$相切时，切点即为所求的点$C$（想一想为什么？）此时圆的半径为$\dfrac 52$，半弦长为$\dfrac 32$，所以圆心到弦$AB$的距离为$2$，这也是点$C$到$AB$的距离，从而所求面积为$3$．

更多与最大张角相关的问题见每日一题[317]最大张角问题．