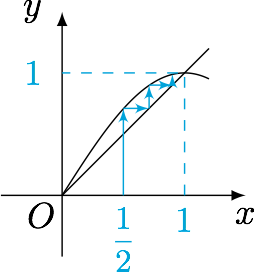这是我在QQ群中国数学解题研究会中看到的问题:
已知数列$\{a_n\}$满足$a_1=\dfrac 12$,$a_{n+1}=\sin\left(\dfrac{\pi}2a_n\right)$($n\in\mathcal N^*$),$S_n$为数列$\{a_n\}$的前$n$项和,求证:$S_n>n-\dfrac 52$.
分析 利用迭代函数研究数列,可得$\{a_n\}$单调递增,极限为$1$,如图.
于是可以考虑利用$1$这个不动点优化递推公式,从而探索可能的放缩方式.
解 根据已知,有$$1-a_{n+1}=1-\sin\left(\dfrac{\pi}2a_n\right),$$令$b_n=1-a_n$,且数列$\{b_n\}$的前$n$项和为$T_n$,则只需要证明$$T_n<\dfrac 52.$$
此时已知条件变为\[\begin{split} b_{n+1}&=1-\sin\left(\dfrac{\pi}2-\dfrac{\pi}2b_n\right) \\ &= 1-\cos\left(\dfrac{\pi}2b_n\right) \\ &=2\sin^2\left(\dfrac{\pi}4b_n\right) \\ &<\dfrac{\pi^2}8\cdot b_n^2\leqslant \dfrac{{\pi}^2}{16}\cdot b_n,\end{split} \]因此$$T_n<\dfrac{\dfrac 12}{1-\dfrac{\pi^2}{16}}=\dfrac{8}{16-\pi^2}<1.305<\dfrac 52,$$原命题得证.