将一堆小球(数量不小于$2$)分为两堆,记录两堆所包含的小球数之积,将这种操作称为“分堆”,将得到的积称为“分堆积”.将一堆包含$n$个小球的小球进行一次“分堆”,对应的“分堆积”设为$p_1$;从得到的两堆小球中选出一堆进行“分堆”,对应的“分堆积”设为$p_2$;再从得到的三堆小球中选出一堆进行“分堆”,对应的“分堆积”设为$p_3$;依次进行下去,直到最后得到$n$堆小球(每堆的小球数量均为$1$)为止.设$$S(n)=p_1+p_2+\cdots +p_{n-1},$$证明:$S(n)$是一个与分堆的具体过程无关的定值.
方法一
每次都分出只包含一个小球的堆,那么有$p_k=n-k$,其中$k=1,2,\cdots ,n-1$.于是$$\sum_{k=1}^{n-1}p_k=(n-1)+(n-2)+\cdots +1=\dfrac 12n(n-1).$$
接下来用数学归纳法证明无论采用何种分法,均有$S(n)=\dfrac 12n(n-1)$,其中$n=2,3,\cdots$.
当$n=2$时,显然有$S(2)=1$,命题成立;
假设命题对$n\leqslant k$($k\geqslant 2,k\in\mathcal N$)都成立,则当$n=k+1$时,记$S(1)=0$,假设经过第$1$次分堆后两堆的小球数分别为$p,n-p$,则\[\begin{split}S(n)&=p (n-p)+S(p)+S(n-p)\\&=p(n-p)+\dfrac 12p(p-1)+\dfrac 12(n-p)(n-p-1)\\&=\dfrac 12\left(2pn-2p^2+p^2-p+n^2-2pn-n+p+p^2\right)\\&=\dfrac 12n(n-1),\end{split}\]因此命题也成立.
综上所述,无论采用何种分法,均有$S(n)=\dfrac 12n(n-1)$,其中$n=2,3,\cdots$.
方法二
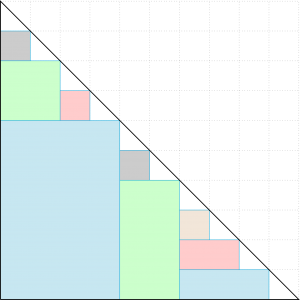
设第一次分堆将$n$个小球分成$a_1$和$a_2$两个部分,那么$$n^2=(a_1+a_2)^2=a_1^2+a_2^2+2a_1a_2,$$可以将这个等式看作$n^2$“分裂”为了$a_1^2$和$a_2^2$,于此同时产生“余项”$2a_1a_2$,也即$2p_1$.随着“分裂”的持续进行直至最终的$n$个$1^2$,所产生的“余项”之和为$$2p_1+2p_2+\cdots 2p_{n-1}=2S(n),$$因此我们有$$n^2=\underbrace{1^2+1^2+\cdots +1^2}_{n}+2S(n),$$即$$S(n)=\dfrac 12n(n-1).$$
如图,所有矩形的面积之和即$S(n)$.
方法三
设$T_n=\{A_1,A_2,\cdots ,A_n\}$为$n$元集合,将第一次分堆视为对集合$T_n$作分划,设分划的结果为$B_s,B_t$,其中$t+s=n$,则满足$x\in B_s$且$y\in B_t$的二元集合$\{x,y\}$的数目即$p_1$,类似地持续进行分划,直到所有集合均为单元素集为止,则所有的二元集合$\{x,y\}$的数目即$S(n)$,且这些二元集合的数目恰好为集合$T_n$的二元子集的个数,因此$$S(n)={\rm C}_n^2=\dfrac 12n(n-1).$$
这个方法也有一个优美的几何解释:
如图,分步将$n$阶(图中以$n=10$为例)完全图中的线逐步擦除即得.
注 整理自程汉波老师的博客(点击这里).