每日一题[324]移花接木

已知实数$a,b,c$ 满足条件$0\leqslant a+c-2b\leqslant 1$且 $2^a+2^b\leqslant 2^{1+c}$．则$\dfrac{2^a-2^b}{2^c}$的取值范围是_____．

---

本题答案是$\left[-\dfrac{1}{4},\dfrac{5-\sqrt{17}}{2}\right]$．

解　注意到$2^a+2^b\leqslant 2^{1+c}$ 即

$$2^{a-c}+2^{b-c}\leqslant 2,$$ 而$\dfrac{2^a-2^b}{2^c}=2^{a-c}-2^{b-c}$，于是令 $$2^{a-c}=m,2^{b-c}=n,$$ 则 $m>0,n>0$． 由$0\leqslant a+c-2b\leqslant 1$得 $$0\leqslant (a-c)-2(b-c)\leqslant 1,$$ 也即 $$2^0\leqslant \dfrac{2^{a-c}}{\left(2^{b-c}\right)^2}\leqslant 2^1.$$ 于是 $$n^2\leqslant m\leqslant 2n^2,$$ 又 $m+n\leqslant 2$， 本题就是在 $$\begin{cases} m>0,n>0,\\m+n\leqslant 2,\\n^2\leqslant m\leqslant 2n^2.\end{cases}$$ 的限制条件下求$m-n$的取值范围．如图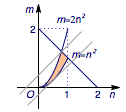： 容易计算得 $$m-n\in\left[-\dfrac{1}{4},\dfrac{5-\sqrt{17}}{2}\right].$$ 在多参数问题中，根据题目的条件与所求结论进行合理换元，对题目进行转化，减少参数个数，是一种常见的处理思路．