2015年北京市海淀区高三期中理科数学试题第14题:
对于数列$\{a_n\}$,若对任意$m,n\in\mathcal N^*\land m\neq n$,都有$\dfrac{a_m-a_n}{m-n}\geqslant t$($t$为常数)成立,则称数列$\{a_n\}$具有性质$P(t)$.
(1)若数列$\{a_n\}$的通项公式为$a_n=2^n$,且具有性质$P(t)$,则$t$的最大值为_______;
(2)若数列$\{a_n\}$的通项公式为$a_n=n^2-\dfrac an$,且具有性质$P(10)$,则实数$a$的取值范围是_______.
正确答案是(1)$2$;(2)$[36,+\infty)$.
解 不妨设$m>n$,于是$P(t)$即$$\forall m,n\in \mathcal N^*\land m>n,a_m-a_n\geqslant tm-tn,$$即$$\forall m,n\in\mathcal N^*\land m>n,a_m-tm\geqslant a_n-tn,$$即$\{a_n-tn\}$是不减的数列.而数列$\{a_n-tn\}$的差分$$\Delta\left(a_n-tn\right)=\Delta a_n-t,$$其中$n\in\mathcal N^*\land n\geqslant 2$.因此性质$P(t)$即数列$\{a_n\}$的差分$\{\Delta a_n\}$有下界$t$.
(1)考虑数列$\{a_n\}$的差分$$\Delta a_n=2^n-2^{n-1}=2^{n-1},$$其中$n\in\mathcal N^*\land n\geqslant 2$,其最小值为$2$,因此$t$的最大值为$2$.
(2)数列$\{a_n\}$的差分$$\begin{split} \Delta a_n&=n^2-\dfrac an-\left[(n-1)^2-\dfrac{a}{n-1}\right]\\&=2n-1+\dfrac{a}{n(n-1)}, \end{split} $$根据题意,有$$\forall n\in\mathcal N^*\land n\geqslant 2,2n-1+\dfrac{a}{n(n-1)}\geqslant 10,$$即$$\forall n\in\mathcal N^*\land n\geqslant 2,a\geqslant n(n-1)(11-2n).$$
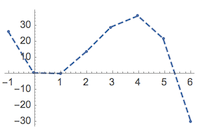
如图,可以根据零点$n=0,1,\frac{11}2$勾勒数列$b_n=n(n-1)(11-2n)$的散点图形成的折线形状.因此右侧的最大值为$$\max\{b_2,b_3,b_4,b_5\}=\max\{14,30,36,20\}=36,$$于是$a$的取值范围是$[36,+\infty)$.
点评 类比于利用导数研究函数的单调性以及最值,数列$\{a_n\}$的差分$$\Delta a_n=a_n-a_{n-1},$$其中$n\in\mathcal N^*\land n\geqslant 2$是研究数列的单调性,进而研究其有界性的重要方法(第(1)小题的解决).同时在研究数列的性质时,也要充分利用其函数本质,在注意其离散特性的同时利用图象辅助解题(第(2)小题的解决).