每日一题[33] 交点曲线系

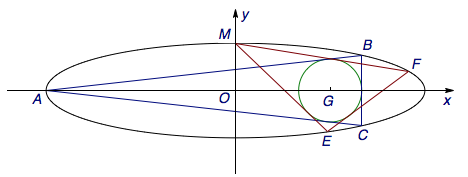
如图，已知圆\(G:(x-2)^2+y^2=r^2\)是椭圆\(\dfrac{x^2}{16}+y^2=1\)的内接三角形\(ABC\)的内切圆，其中\(A\)为椭圆的左顶点．

（1）求圆\(G\)的半径\(r\)；

（2）过\(M(0,1)\)作圆的两条切线交椭圆于\(E,F\)两点，证明：直线\(EF\)与圆\(G\)相切．

 （1）如图，设切点分别为\(P,Q\)．

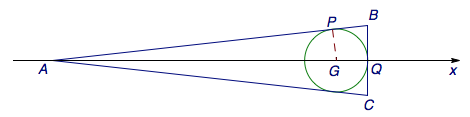
由三角形\(APG\)与三角形\(AQB\)相似，有\[\frac{PG}{AP}=\frac{BQ}{AQ},\]于是\[\frac{r}{\sqrt{36-r^2}}=\frac{BQ}{6+r},\]从而\[BQ=r\cdot\sqrt{\frac{6+r}{6-r}}.\]

将\(B\)的坐标代入椭圆方程有\[\frac{1}{16}\cdot (2+r)^2+\left(r\cdot\sqrt{\frac{6+r}{6-r}}\right)^2=1,\]注意到\(r=-6\)是该方程的一个解，解得正根\[r=\frac 23.\]

（2）设过\(M\)的切线为\(y=kx+1\)，则由直线与圆的位置关系可得\[\frac{\left|2k+1\right|}{\sqrt{1+k^2}}=\frac 23,\]即\[32k^2+36k+5=0.\]

于是设直线\(ME\)、\(MF\)的斜率分别为\(k_1\)、\(k_2\)，则\[k_1+k_2=-\frac{9}{8},k_1\cdot k_2=\frac 5{32}\qquad\cdots (*).\]

将两条相交直线\(ME\cup MF\)看作是一条曲线\[\left(y-k_1x-1\right)\cdot\left(y-k_2x-1\right)=0,\]

注意到这条曲线与椭圆的交点为\(M\)、\(E\)、\(F\)，因此需要设法联立变形为直线方程，且在联立过程中去掉解\(x=0,y=1\)．

于是将该曲线方程和椭圆方程分别变形为\[-k_1\cdot k_2x^2=(y-1)^2-(k_1+k_2)x(y-1)\]和\[-\frac 1{16}x^2=y^2-1,\]

将(*)代入，两式相比得\[\frac 52=\frac{y-1+\frac 98x}{y+1},\]化简得\[EF:9x-12y-28=0.\]

从而圆心\(G(2,0)\)到直线\(EF\)的距离为\[\frac{10}{\sqrt{9^2+12^2}}=\frac 23=r,\]原命题得证．

点评    有大量三线共点时考虑交点曲线系是非常正确的选择，如何根据要求书写交点曲线系是其中富有技巧性的部分．例如本题中就没有使用平时熟知的交点曲线系\(F+\lambda G=0\)．