每日一题[276] 独立的空间向量

下面这道试题是很多教辅书上都有的经典试题：

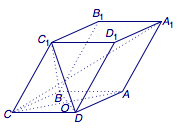
如图，已知平行六面体$ABCD-A_1B_1C_1D_1$的底面是菱形且从顶点$C$出发的三条棱两两形成的角$\angle C_1CB=\angle C_1CD=\angle BCD=60^\circ$，

（1）证明：$C_1C\perp BD$；

（2）当$\dfrac{CD}{CC_1}$的值为多少时，可使$A_1C\perp C_1BD$？

（1）证明    连接$AC$交$BD$于$O$，则由底面$ABCD$为菱形可得对角线$AC$与$BD$互相垂直平分．

由$\triangle C_1CD$与$\triangle C_1CB$全等，可得$C_1D=C_1B$，进而$\triangle C_1BD$为等腰三角形，于是$C_1O\perp BD$（三线合一）．

综上，$BD\perp C_1CAA_1$，因此$BD\perp C_1C$．

（2）解    由于无论$\dfrac{CD}{CC_1}$的值如何变化，$A_1C$始终与$BD$保持垂直，于是只需要使得$A_1C$与平面$C_1BD$内的其他与$BD$不平行的直线（如$C_1O$）垂直即可．但接下来无论是对截面$AA_1C_1C$进行分析（几何）还是建立空间直角坐标系进行研究（代数）运算量都较大，我们可以采用同时融合几何与代数特性与一身的空间向量解决问题．

记$\overrightarrow{CB}={\bf a}$，$\overrightarrow{CD}={\bf b}$，$\overrightarrow{CC_1}={\bf c}$，且它们的模分别为$1$、$1$、$x$．

令$\overrightarrow{CA_1}\cdot \overrightarrow {C_1D}=0$得 $$\left({\bf a}+{\bf b}+{\bf c}\right)\cdot\left({\bf b}-{\bf c}\right)=0,$$ 即 $${\bf a}\cdot{\bf b}-{\bf a}\cdot{\bf c}+{\bf b}\cdot{\bf b}-{\bf c}\cdot{\bf c}=0,$$ 由已知，不难得到 $$\dfrac 12-\dfrac 12x+1-x^2=0,$$ 解得 $$x=1.$$

注    建系坐标计算是利用空间向量解决立体几何问题的一种方式，但并不是唯一的方式．空间向量完全可以脱离空间直角坐标系独立运作，尤其是当基本架构中的关键角度并非直角时直接利用空间向量进行计算往往更为简便．