2013年高考浙江卷理科数学第16题(填空压轴题):
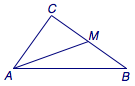
在三角形\(ABC\)中,\(\angle C=90^\circ\),\(M\)是\(BC\)的中点,若\(\sin\angle BAM=\dfrac 13\),则\(\sin\angle BAC=\)_______.
正确答案是\(\dfrac{\sqrt 6}3\).
解 恰当的将条件\(MB=MC\)转化是解决问题的关键.考虑到\(C\)为直角,因此\[\tan\angle BAC=2\tan\angle MAC,\]即\[\begin{eqnarray}\tan\angle BAC=2\tan\left(\angle BAC-\angle BAM\right).\end{eqnarray}\]
由\(\sin\angle BAM=\dfrac 13\),得\[\tan\angle BAM=\dfrac{\sqrt 2}4,\]代入(1)中,得\[\tan\angle BAC =2\cdot\dfrac{\tan\angle BAC-\frac{\sqrt 2}4}{1+\tan\angle BAC\cdot\frac{\sqrt 2}4},\]解得\[\tan \angle BAC=\sqrt 2,\]于是可得\[\sin\angle BAC=\dfrac{\sqrt 6}3.\]
在解方程的时候注意到方程关于\(\tan\angle BAC\)有重根.这就意味着如果随着条件\(\angle BAM\)的改变,那么\(\tan \angle BAC\)可能无解,可能有一解,也可能有两解.这样一来,就有对几何图形作进一步探索的必要了.
为了方便探索,可以将问题转化为当\(\angle BAC\)变化时,\(\angle MAB\)的取值范围.
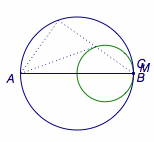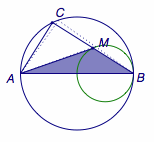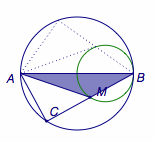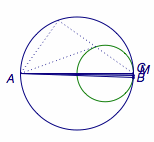
如图,固定三角形\(ABC\)的斜边\(AB\),使直角顶点\(C\)在圆上运动,此时\(BC\)边的中点\(M\)运动的轨迹也为圆(\(M\)的轨迹以\(B\)为中心缩小到\(\dfrac 12\)的结果).
易得当直线\(AM\)与点\(M\)的轨迹相切时(图中的虚线位置)\(\angle MAB\)最大,其最大值恰为\(\arcsin\dfrac 13\),即本文题中所给出的条件.
这样,我们就得到了当\(\sin\angle MAB>\dfrac 13\)时,无解;当\(\sin\angle MAB=\dfrac 13\)时,一解;当\(0<\sin\angle MAB<\dfrac 13\)时,两解.
注 题中推广问题以及图形构造由江苏无锡王举老师提供.