每日一题[26] 好一个分段函数

今天继续昨天的问题，讨论较为复杂的方程的根的个数．

讨论关于$x$的方程 $$\left|x+\dfrac 1x\right|-\left|x-\dfrac 1x\right|=kx+1$$ 的根的个数．

原方程的根的个数即函数$y=\left|x+\dfrac 1x\right|-\left|x-\dfrac 1x\right|$与直线$y=kx+1$的交点个数．

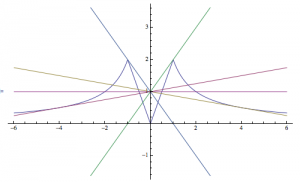
利用处理包含绝对值的函数的零点分段讨论法，不难将函数化简为 $$y=\begin{cases}-\dfrac 2x,&x<-1\\-2x,&-1\leqslant x<0\\2x,&0<x\leqslant 1\\\dfrac 2x,&x>1\end{cases}$$ 进而画出函数的草图．另一方面，直线$y=kx+1$恒过定点$(0,1)$，如图．

经计算（利用导数或者联立都可以），可知其中的分界点为 $$-1,-\dfrac 18,0,\dfrac 18,1,$$ 因此梳理出答案，根的个数为 $$\begin{cases}1,&k\in(-\infty,-1)\cup(1,+\infty),\\2,&k\in\{-1,1\},\\3,&k\in \left(-1,-\dfrac 18\right)\cup \left(\dfrac 18,1\right)\\4,&k\in\left\{-\dfrac 18,0,\dfrac 18\right\}\\5,&k\in \left(-\dfrac 18,0\right)\cup \left(0,\dfrac 18\right)\end{cases}.$$

注    $0$这个分界点很隐蔽哦！