函数不等式相关的问题解决思路通常是“通过函数的单调性将函数不等式转化成自变量相关的不等式”,但有时函数的单调区间比较复杂,直接用单调性无法解决问题,这时往往就需要借助函数的图象寻找突破口了.
2013年天津高考理科第8题(选择压轴题):
已知函数\(f(x)=x(1+a|x|)\),设关于\(x\)的不等式\(f(x+a)<f(x)\)的解集为\(M\),若\(\left[-\dfrac 12,\dfrac 12\right]\subseteq M\),则实数\(a\)的取值范围是____.
本题答案是\(\left(\dfrac{1-\sqrt 5}{2},0\right)\).
解 首先我们能得到\(f(x)\)为奇函数,单调区间的情况与\(a\)的正负有关,且\(a\ne 0\).
当\(a>0\)时,\(f(x)\)在\(\mathcal{R}\)上单调递增,不等式不可能成立.
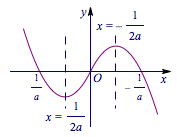
所以\(a<0\),此时\(f(x)\)的草图如下(可以先画出\([0,+\infty)\)的部分再对称过来)
此函数在整个定义域上没有单调性,无法直接将函数不等式转化成与自变量相关的不等式,
我们需要从函数的图象出发,看看函数不等式\(f(x+a)<f(x)\)有什么直观意义:
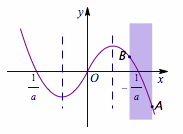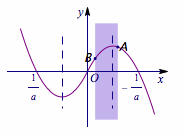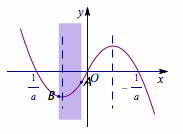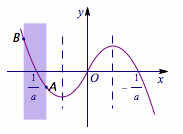
取\(A(x,f(x))\),\(B(x+a,f(x+a))\),当\(A\)点与\(B\)点在函数图象上变动时,点\(B\)在点\(A\)的下方时对应的\(A\)点的横坐标满足函数不等式,如图:
因为\(x=0\)时,不等式成立,所以我们有\(f(a)<0\),故\(a>\dfrac 1a\),解得\(-1<a<0\).
从而\(-\dfrac{1}{2a}>\dfrac 12\),结合图象知要满足\(\left[-\dfrac 12,\dfrac 12\right]\subseteq M\),只需考虑\(x=-\dfrac 12\)的情况即可,当\(\dfrac{-\dfrac 12-\dfrac 12+a}{2}>\dfrac{1}{2a}\)时,有\(f\left(-\dfrac 12+a\right)<f\left(-\dfrac 12\right)\),解得\(a>\dfrac{1-\sqrt 5}{2}\).
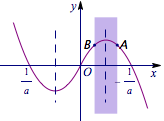
事实上我们可以找到满足条件的点\(A\)的两个边界情况,如下:
可以得到集合\(M=\left(\dfrac{1}{2a}-\dfrac a2,-\dfrac{1}{2a}-\dfrac a2\right)\).
注 类似问题见 每日一题[221] 愚公移山.