每日一题[17] 向量转转转

本题是2015年北京市北京大学附属中学的高一期末填空题的最后一题，综合考察了平面向量、递推（归纳）思想以及对新定义的理解与应用．对于没有学过复数的高一的学生来说，这道题还是颇有难度的，细细品来也别有一番风味．

设系列向量\(\overrightarrow{a_n}\left(n\in\mathcal N\right)\)按如下方式形成：

\(\overrightarrow{a_0}=\left(5,0\right)\)，常向量\(\overrightarrow b=\left(10,0\right)\)；

\(\overrightarrow{a_0}\)绕起点逆时针旋转\(\dfrac{\pi}4\)，得到向量\(\overrightarrow{b_0}\)，\(\overrightarrow{a_1}=\overrightarrow{b_0}+\overrightarrow b\)；

\(\overrightarrow{a_1}\)绕起点逆时针旋转\(\dfrac{\pi}4\)，得到向量\(\overrightarrow{b_1}\)，\(\overrightarrow{a_2}=\overrightarrow{b_1}+\overrightarrow b\)；

……  ……

\(\overrightarrow{a_n}\)绕起点逆时针旋转\(\dfrac{\pi}4\)，得到向量\(\overrightarrow{b_n}\)，\(\overrightarrow{a_{n+1}}=\overrightarrow{b_n}+\overrightarrow b\)．

则\(\left|\overrightarrow{a_{2015}}\right|=\)________．

注：“绕起点”这个限制是多余的．

正确答案是\(5\)．

我们用\(\overrightarrow a\angle\theta\)表示将\(\overrightarrow a\)逆时针旋转\(\theta\)角后所得到的新向量，则这种新运算有性质1\[\left(\overrightarrow a+\overrightarrow b\right)\angle\theta=\overrightarrow a\angle\theta+\overrightarrow b\angle\theta,\]以及性质2\[\overrightarrow a\angle\alpha\angle\beta=\overrightarrow a\angle \left(\alpha+\beta\right).\]于是\[\begin{split}\overrightarrow{a_n}&=\overrightarrow{b_{n-1}}+\overrightarrow b\\&=\overrightarrow{a_{n-1}}\angle\dfrac{\pi}4+\overrightarrow b\\&=\left(\overrightarrow{a_{n-2}}\angle\dfrac{\pi}4+\overrightarrow b\right)\angle\dfrac{\pi}4+\overrightarrow b\\&=\overrightarrow{a_{n-2}}\angle\dfrac{2\pi}4+\overrightarrow b\angle\dfrac{\pi}4+\overrightarrow b\\&=\cdots\\&=\overrightarrow{a_0}\angle\dfrac{n\pi}4+\overrightarrow b\angle\dfrac{\left(n-1\right)\pi}4+\overrightarrow b\angle\dfrac{\left(n-2\right)\pi}4+\cdots+\overrightarrow b.\end{split}\]当\(n=2015\)时，有\[\begin{split}\overrightarrow{a_{2015}}&=\overrightarrow{a_0}\angle\dfrac{2015\pi}4+\overrightarrow b\angle\dfrac{2014\pi}4+\overrightarrow b\angle\dfrac{2013\pi}4+\cdots+\overrightarrow b\\&=\overrightarrow{a_0}\angle\dfrac{2015\pi}4-\overrightarrow b\angle\dfrac{2015\pi}4+\underbrace{\overrightarrow b\angle\dfrac{2015\pi}4+\overrightarrow b\angle\dfrac{2014\pi}4+\overrightarrow b\angle\dfrac{2013\pi}4+\cdots+\overrightarrow b}_{\overrightarrow 0}\\&=\left(\overrightarrow{a_0}-\overrightarrow b\right)\angle\dfrac{2015\pi}4.\end{split}\]

下图为上述计算中连续\(2016\)个向量的和为零向量的解释：

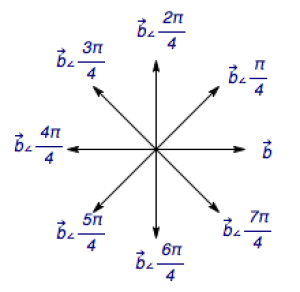
因此\[\left|\overrightarrow{a_{2015}}\right|=\left|\overrightarrow{a_0}-\overrightarrow b\right|=5.\]