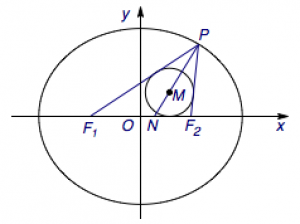
已知\(P\)为椭圆\(\dfrac{x^2}4+\dfrac{y^2}3=1\)上一点,\(F_1\)、\(F_2\)分别为椭圆的两个焦点,圆\(M\)为三角形\(F_1PF_2\)的内切圆圆心,\(PM\)交\(x\)轴于\(N\),求\(\dfrac{PM}{MN}\)的值.
 设\(P\)到\(x\)轴的距离为\(h\),内切圆的半径为\(r\),则
设\(P\)到\(x\)轴的距离为\(h\),内切圆的半径为\(r\),则
\[S_{\triangle PF_1F_2}=\dfrac 12(2a+2c)\cdot r=\dfrac 12\cdot (2c)\cdot h.\]
因此\[\dfrac{PN}{MN}=\dfrac hr=\dfrac {a+c}c,\]
于是\[\dfrac{PM}{MN}=\dfrac{PN-MN}{MN}=\dfrac{PN}{MN}-1=\dfrac ac=2.\]