已知锐角\(\triangle ABC\)中，以\(BC\)为直径作\(\bigodot O\)，\(AD\)切\(\bigodot O\)于点\(D\)，\(E\)为\(AB\)上一点，作\(EF\perp AB\)交\(AC\)延长线于点\(F\)，若\(AB\cdot AC=AE\cdot AF\)，求证：\(AD=AE\)．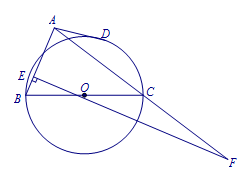
证明 设\(\bigodot O\)与\(AB\)的交点为\(G\)，连接\(CG\)，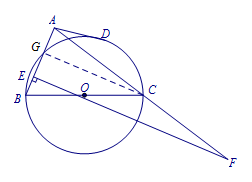
则\[CG\perp AB.\]又\[EF\perp AB,\]所以\[\dfrac {AG}{AE}=\dfrac {AC}{AF}.\]而\[AB\cdot AC=AE\cdot AF,\]所以\[\dfrac {AE}{AB}=\dfrac {AG}{AE}.\]即\[AE^2=AB\cdot AG.\]由圆幂定理，有\[AD^2=AG\cdot AB,\]所以\[AD=AE.\]