已知平面上两点\(A,B\)，则所有满足\(\dfrac {PA}{PB}=k\)且不等于\(1\)的点\(P\)的轨迹是一个圆，这个轨迹最先由古希腊数学家阿波罗尼斯发现，故称阿氏圆，又称阿波罗尼斯圆．（当\(k=1\)时，点\(P\)的轨迹为\(AB\)的垂直平分线．）
我们可以用代数、几何两种方法来证明该结论．
（1）代数方法
设定\(AB=1\)．如图所示，以点\(A\)为原点建立平面直角坐标系，则\(A(0,0)\)，\(B(1,0)\)．
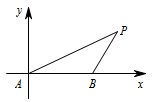令点\(P\)坐标为\((x,y)\)，则由题意可得\[\dfrac {\sqrt{x^2+y^2}}{\sqrt{(x-1)^2+y^2}}=k,\]整理得\[\left(x-\dfrac {k^2}{k^2-1}\right)^2+y^2=\left(\dfrac k{k^2-1}\right)^2.\]所以点\(P\)的轨迹是一个圆．
该圆与直线\(AB\)有两个交点，以这两点的中点为圆心，两点距离的一半为半径即可画出此圆．
如图，动点\(P\)的轨迹是以\(CD\)为直径的圆，其中\(\dfrac {CA}{CB}=\dfrac {DA}{DB}=k\)．
（2）几何方法
如图，在直线\(AB\)上有且只有两点\(C,D\)，使得\(\dfrac {CA}{CB}=\dfrac {DA}{DB}=k\)．
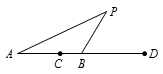此时，\(\dfrac {CA}{CB}=\dfrac {PA}{PB}=k\)．
我们知道，三角形一个角的平分线分其对边所成的两条线段与这个角的两边对应成比例；它的逆命题依然成立．下面来证明这个结论：
连接\(PC\)，过点\(C\)作\(CE\parallel BP\)交\(AP\)于点\(E\)．
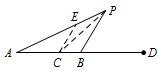\(\because CE\parallel BP\)，
\(\therefore \dfrac {AC}{CB}=\dfrac {AE}{EP}\)，\(\dfrac {AP}{PB}=\dfrac {AE}{EC}\)．
\(\because \dfrac {AC}{CB}=\dfrac {AP}{PB}\)，
\(\therefore \dfrac {AE}{EP}=\dfrac {AE}{EC}\)，
\(\therefore EP=EC\)，
\(\therefore \angle APC=\angle ECP=\angle CPB\)，
即\(PC\)为\(\triangle ABP\)的角平分线．
同样，三角形一个角的外角平分线外分对边所成的两条线段与相邻两边对应成比例；反之亦成立．
连接\(PD\)，过点\(D\)作\(DF\parallel BP\)交\(AP\)的延长线于点\(F\)．
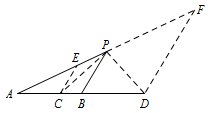证明同上，即\(\angle BPD=\angle DPF\)．
此时\(\angle CPD=\angle CPB+\angle BPD=90^\circ\)．
即点\(P\)在以\(CD\)为直径的圆上（除\(C,D\)两点外）．
反过来，该圆上的所有点均满足到线段\(AB\)两端点的距离之比为定值．
所以满足条件的点\(P\)的轨迹是一个圆．
练习 如图，在等腰\(\triangle ABC\)中，\(AB=AC\)，\(BD\)是腰\(AC\)的中线，且\(BD=\sqrt 3\)，则\(S_{\triangle ABC}\)的最大值是\(\underline{\qquad}\)．
正确答案为\(2\)．
由已知条件，可得\(BD\)为定长线段，\(\dfrac {AB}{AD}=2\)为定值，故点\(A\)的轨迹即为一个阿波罗尼斯圆，即以\(EF\)为直径的圆，其中\(E,F\)满足\(\dfrac {BE}{ED}=\dfrac {BF}{FD}=2\)．
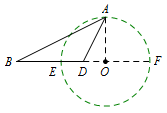如图所示，连接\(AO\)，当\(AO\perp BD\)时，\(S_{\triangle ABD}\)取最大值\(1\)，即\(S_{\triangle ABC}\)的最大值是\(2\)．