巧用辅助圆，做题更简单！

如图，$\angle B=\angle CDE=90^\circ$，$BC=6$，$AB=8$，求$BD$为何值时$CE$最短，并求出$CE$的最小值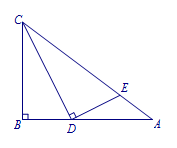．方法一：　注意到动点$D$在运动时，$\angle CDE=90^\circ$是不变量，那么点$D$在以$CE$为直径的圆上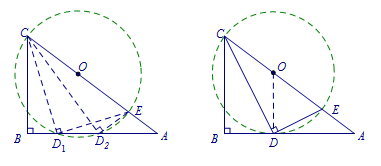． 比较上面两图可知，当且仅当$\odot O$与$AB$相切时，半径$OD$最小． 连接$OD$， 易证 $$\triangle AOD \backsim {\triangle ACB}，$$ 所以 $$\dfrac {AO}{AC}=\dfrac {DO}{BC}.$$ 解得 $$r=\dfrac {15}4．$$ 即$CE$的最小值为$7.5$．
方法二：　当看到图中两个直角的顶点都在线段$AB$上时，易想到如图构造“一线三等角”相似模型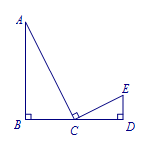．故作$EH\perp AB$，垂足为$H$，易得 $$\triangle DEH \backsim {\triangle CDB}，\\ \triangle AEH \backsim {\triangle ACB}，$$ 设${EH}=3x$，${AH}=4x$，${AE}=5x$,${BD}=y$,${DH}=8-4x-y$,${CE}=10-5x$, 即有 $$\dfrac {3x}{y}=\dfrac {8-4x-y}{6}，$$ 整理，得 $$y^2-(8-4x)y+18x=0,$$ 关于$y$的一元二次方程有根，得 $$\Delta \geqslant 0,$$ 解得 $$0<x \leqslant \dfrac 12 \ \ 或\ x\geqslant 8（舍）.$$ 所以 $$CE\geqslant \dfrac {15}2.$$ 即$CE$的最小值为$7.5$．
在遇到动点问题时我们要多注意这些不变量，此题两种方法中利用辅助圆就比代数方法简便很多，所以值得大家推广学习．