每日一题[130] 构造原函数

若$f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)$，其中$a\leqslant b\leqslant c$，对于下列结论：

① $f(b)\leqslant 0$；

② 若$b=\dfrac{a+c}2$，则$\forall x\in\mathcal R,f(x)\geqslant f(b)$；

③ 若$b\leqslant \dfrac{a+c}2$，则$f(a)\leqslant f(c)$；

④ $f(a)=f(c)$成立的充要条件为$b=0$．

其中正确的是_______．

---

正确答案是①②③．

注意到

$$f(x)=\left[(x-a)(x-b)(x-c)\right]',$$ 于是$f(b)$即函数 $$F(x)=(x-a)(x-b)(x-c)$$ 在$x=b$处的切线斜率，结合三次函数图象的对称性易得．

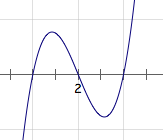
例如对于②，根据三次函数图象的对称性，$(b,0)$为对称中心，于是命题正确，如图：

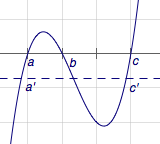
再比如对于③，根据三次函数图象的对称性，若$b<\dfrac{a+c}{2}$，则对称中心必然在$x$轴下方．过对称中心作$x$轴的平行线，于三次函数图象交于除对称中心以外的两点，设该两点的横坐标分别为$a',c'(a'<c')$，则

$$F'(a)<F'(a')=F'(c')<F'(c),$$ 因此命题正确．如图：

---

留一个高考题作为练习．

（2013年·重庆）若$a<b<c$，则函数

$$f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)$$ 的两个零点分别位于区间（        ）

A．$(a,b)$和$(b,c)$内

B．$(-\infty,a)$和$(a,b)$

C．$(b,c)$和$(c,+\infty)$

D．$(-\infty,a)$和$(c,+\infty)$

正确的答案是A．