练习题集[70]基础练习

1．若存在实数$a$使得$|x+a|\leqslant \ln x+1$在$x\in [1,m]$上恒成立，则$m$的最大正整数值为_______．

2．不超过$\left(\sqrt 5+\sqrt 3\right)^6$的最大整数是_______．

3．设$2016$次多项式$f(x)$满足$f(k)=\dfrac{1}{{\rm C}_{2016}^k}$($k=0,1,2,\cdots ,2016$)，则$f(2017)=$_______．

4．已知数列$\{a_n\}$满足$0<a_n<1$，求证： $$a_1(1-a_1)+(a_2-a_1)(1-a_2)+(a_3-a_2)(1-a_3)+\cdots +(a_n-a_{n-1})(1-a_n)<\dfrac 12.$$

5．数列$\{a_n\}$满足$a_1=1$，$a_{n+1}=a_n+\dfrac{1}{[a_n]}$，求$\{a_n\}$的通项公式．

6．一个四边形的三边分别为$2,7,11$，求该四边形面积的最大值．

7．设$a,b$都是正整数，求$\left|12^a-5^b\right|$的最小值．

参考答案

1．参数$a$的值控制着函数$y=|x+a|$的图象的左右移动．因此当$-a$增大时，对应的$m$也相应增大．当$y=|x+a|$的“左翼”过$y=\ln x+1$上的点$(1,1)$时，$-a$最大，此时使得题中不等式成立的范围的“上限”最大，如图．不难求得$m$的最大正整数值为$4$．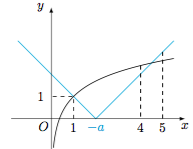
2．设$a=\sqrt 5+\sqrt 3$，$b=\sqrt 5-\sqrt 3$，则 $$a^2+b^2=16,a^2b^2=4,$$ 从而
$$a^6+b^6=\left(a^2+b^2\right)^3-3a^2b^2(a^2+b^2)=3904,$$ 又$b^6\in (0,1)$，于是所求的最大整数为$3903$．

3．由拉格朗日插值公式，可得 $$\begin{split} f(2017)&=\sum_{k=0}^{2016}\left[\dfrac{2017!}{k!\cdot (-1)^k\cdot (2016-k)!}\cdot f(k)\right]\\ &=\sum_{k=0}^{2016}\left[\dfrac{2017!}{k!\cdot (-1)^k\cdot (2016-k)!}\cdot \dfrac{k!\cdot (2016-k)!}{2016!}\right]\\ &=2017\sum_{k=0}^{2016}{(-1)^k}=2017.\end{split}$$ 4．根据题意，有 $$\begin{split} LHS&=a_n-\left(a_1^2+a_2^2+a_3^2+\cdots +a_n^2-a_1a_2-a_2a_3-\cdots -a_na_{n-1}\right)\\ &=a_n-\dfrac 12\left[(a_1-a_2)^2+(a_2-a_3)^2+\cdots +(a_{n-1}-a_n)^2\right]-\dfrac 12a_1^2-\dfrac 12a_n^2\\ &<a_n-\dfrac 12a_n^2<\dfrac 12,\end{split}$$ 因此原不等式得证．

5．易知 $$a_n:1,2,2\dfrac 12,3,3\dfrac 13,3\dfrac 23,4,4\dfrac 14,4\dfrac 24,4\dfrac 34,5,\cdots ,$$ 于是 $$a_n=\begin{cases} k,&n=n_0=\dfrac 12\left(k^2-k+2\right),\\k+\dfrac{n-n_0}k=\dfrac{n}{k}+\dfrac{k}{2}+\dfrac 12-\dfrac 1k,&n\in \left(\dfrac 12\left(k^2-k+2\right),\dfrac 12\left(k^2+k+2\right)\right),\end{cases}$$ 其中$k\in\mathcal N^*$，$n=1,2,3,\cdots$．

6．设第四条边的长度为$2x$，我们熟知四边长固定的四边形为圆内接四边形时面积最大，因此根据海伦公式，此时四边形面积的最大值 $$S(x)=\sqrt{(x+8)(x+3)(x-1)(10-x)},$$ 也即 $$S(x)=\sqrt{-x^4+87x^2+154x-240}.$$ 设$\varphi(x)=-x^4+87x^2+154x-240$，其中$x\in (1,10)$， 则其导函数 $$\varphi'(x)=-4x^3+174x+154=-2(x-7)\left(2x^2+14x+11\right),$$ 于是当$x=7$时该函数取得最大值$\varphi(7)=2700$，进而可得所求四边形面积的最大值为$30\sqrt 3$．

下面证明四边长固定的四边形为圆的内接四边形时面积最大，并推导四边形的面积最大值：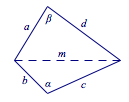
记四边形面积为$S$，则 $$S=\dfrac 12ad\sin\beta+\dfrac 12bc\sin\alpha .$$ 又由余弦定理知 $$m^2=a^2+d^2-2ad\cos\beta=b^2+c^2-2bc\cos\alpha.$$ 于是我们有 $$\begin{cases} bc\cos\alpha -ad\cos\beta =\dfrac {b^2+c^2-a^2-d^2}{2},\\bc\sin\alpha +ad\sin\beta =2S,\end{cases}$$ 两式平方后相加整理得 $$4S^2=b^2c^2+a^2d^2-n^2-2abcd\cos(\alpha +\beta ),$$ 其中$2n=b^2+c^2-a^2-d^2$．所以当$\cos(\alpha +\beta )=-1$时，$S$有最大值，此时四边形为圆的内接四边形．同时面积最大值 $$\begin{split} S_{\max}^2=&\dfrac 14\left[b^2c^2+a^2d^2-\dfrac 14(b^2+c^2-a^2-d^2)^2+2abcd\right ]\\=&\dfrac{1}{16}(b+c+d-a)(b+c+a-d)(a+b+d-c)(a+c+d-b).\end{split}$$  

7．所求的最小值为$7$．证明如下．

首先，由于$\left|12^a-5^b\right|\equiv 1\pmod 2$，于是$\left|12^a-5^b\right|$的最小值不可能是$0,2,4,6$．

进而，由于$3\mid 12^a$而$3 \nmid 5^ b$，于是$\left|12^a-5^b\right|$的最小值不可能是$3$；类似的，$5\nmid 12^a$而$5 \mid 5^ b$，于是$\left|12^a-5^b\right|$的最小值不可能是$5$．

接下来，若$12^a-5^b=1$，那么$12^a-1=5^b$，而$11\mid \left(12^a-1\right)$且$11\nmid 5^b$，矛盾．因此$12^a-5^b\ne 1$．

最后，若$12^a-5^b=-1$，那么$12^a=5^b-1$，则有 $$12^a\equiv 4\pmod 5,$$ 即$2^{a-2}\equiv 1\pmod 5$，从而$a=4n+2$($n\in\mathcal N$)，于是 $$144^{2n+1}+1=5^b,$$ 而$145\mid \left(144^{2n+1}+1\right)$且$145\nmid 5^b$，矛盾．因此$12^a-5^b\ne -1$．

综上所述，$\left|12^a-5^b\right|$的最小值为$7$．