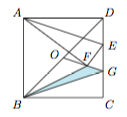
1.如图,在正方形$ABCD$中,$AB=6$,点$E$在边$CD$上,$DE=\dfrac 13DC$.连接$AE$,将$\triangle ADE$沿$AE$翻折,点$D$落在$F$处.点$O$是对角线$BD$的中点,连接$OF$并延长交$CD$于点$G$,连接$BF,BG$,则$\triangle BFG$的周长是_____.
2.设正数$x,y,z$满足$x^2+y^2+z^2=1$,求证:$\dfrac{xy}z+\dfrac{yz}x+\dfrac{zx}y\geqslant \sqrt 3$.
3.已知$a,b,c>0$,求证:$\dfrac{1}{a^3+b^3+abc}+\dfrac{1}{b^3+c^3+abc}+\dfrac{1}{c^3+a^3+abc}\leqslant \dfrac{1}{abc}$.
4.(2016年全国高中数学联赛安徽省初赛第11题)已知$a,b,c\in\mathcal R$,求证:$$\sqrt{a^2+ab+b^2}+\sqrt{a^2+ac+c^2}\geqslant\sqrt{3a^2+(a+b+c)^2},$$并指出等号取得的条件.
5.已知$a,b$均为正实数,求证:$\dfrac{b^2+2}{a+b}+\dfrac{a^2}{ab+1}\geqslant 2$.
6.已知数列$\{a_n\}$中$a_1=1$,$a_2=2$,$a_{n+2}=a_n+a_{n+1}$($n\in\mathcal N^*$),求证:$a_{n+1}^{\frac 1n}\geqslant 1+a_n^{-\frac 1n}$($n\in\mathcal N^*$).
7.已知参数方程$\Gamma:\begin{cases} x=\dfrac{t^2-2t}{t^2+1},\\ y=\dfrac{-t-2}{t^2+1},\end{cases} $其中$t$为参数且$t\in\mathcal R$,判断参数方程$\Gamma$表示何种二次曲线,并求其对称轴方程及离心率.
参考答案
1.由于$O$点和$D$点到直线$AE$的距离相等,于是$OG\parallel AE$,从而$G$点也是$CD$的一个三等分点,且$CG=2$.如图,连接$DF$,作$FH\perp BC$于$H$,则$DF\perp OG$.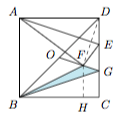 由于$AD=6$,$DE=2$,于是$D$到$AE$的距离为$\dfrac{6}{\sqrt{10}}$,因此$DF=\dfrac{12}{\sqrt{10}}$,进而可得$FG=\dfrac{4}{\sqrt{10}}$.进而由$OG=\dfrac 12AE=\sqrt{10}$,得$\dfrac{GF}{GO}=\dfrac 25$.于是有$$\dfrac{BH}{BC}=1-\dfrac{CH}{CB}=1-\dfrac 12\cdot \dfrac{GF}{GO}=\dfrac 45,$$类似的,有$\dfrac{FH}{DC}=\dfrac 25$,从而$$BF=\dfrac{2\sqrt 5}5\cdot AB=\dfrac{12\sqrt 5}5.$$因此$\triangle BFG$的周长为$$BF+FG+BG=\dfrac{12\sqrt 5}5+\dfrac{2\sqrt{10}}{5}+2\sqrt{10}=\dfrac{12\big(\sqrt 5+\sqrt {10}\big)}5.$$2.证明 考虑到欲证的不等式左边为一次式,尝试先平方.\[\begin{split} \left(\dfrac{xy}z+\dfrac{yz}x+\dfrac{zx}y\right)^2&=\dfrac{x^2y^2}{z^2}+\dfrac{y^2z^2}{x^2}+\dfrac{z^2x^2}{y^2}+2(x^2+y^2+z^2)\\& \geqslant \dfrac{xy}z\cdot \dfrac{yz}x+\dfrac{yz}x\cdot \dfrac{zx}y+\dfrac{zx}y\cdot \dfrac{xy}z+2(x^2+y^2+z^2)\\ &=3(x^2+y^2+z^2)=3,\end{split} \]因此原不等式得证.
由于$AD=6$,$DE=2$,于是$D$到$AE$的距离为$\dfrac{6}{\sqrt{10}}$,因此$DF=\dfrac{12}{\sqrt{10}}$,进而可得$FG=\dfrac{4}{\sqrt{10}}$.进而由$OG=\dfrac 12AE=\sqrt{10}$,得$\dfrac{GF}{GO}=\dfrac 25$.于是有$$\dfrac{BH}{BC}=1-\dfrac{CH}{CB}=1-\dfrac 12\cdot \dfrac{GF}{GO}=\dfrac 45,$$类似的,有$\dfrac{FH}{DC}=\dfrac 25$,从而$$BF=\dfrac{2\sqrt 5}5\cdot AB=\dfrac{12\sqrt 5}5.$$因此$\triangle BFG$的周长为$$BF+FG+BG=\dfrac{12\sqrt 5}5+\dfrac{2\sqrt{10}}{5}+2\sqrt{10}=\dfrac{12\big(\sqrt 5+\sqrt {10}\big)}5.$$2.证明 考虑到欲证的不等式左边为一次式,尝试先平方.\[\begin{split} \left(\dfrac{xy}z+\dfrac{yz}x+\dfrac{zx}y\right)^2&=\dfrac{x^2y^2}{z^2}+\dfrac{y^2z^2}{x^2}+\dfrac{z^2x^2}{y^2}+2(x^2+y^2+z^2)\\& \geqslant \dfrac{xy}z\cdot \dfrac{yz}x+\dfrac{yz}x\cdot \dfrac{zx}y+\dfrac{zx}y\cdot \dfrac{xy}z+2(x^2+y^2+z^2)\\ &=3(x^2+y^2+z^2)=3,\end{split} \]因此原不等式得证.
3.证明 由于\[\begin{split}\sum_{cyc}\dfrac{abc}{a^3+b^3+abc}&=\dfrac{abc}{(a+b)(a^2-ab+b^2)+abc}\\ &\leqslant \sum_{cyc}\dfrac{abc}{(a+b)\cdot ab+abc}\\&=\sum_{cyc}\dfrac{c}{a+b+c}\\ &=1,\end{split}\]所以原不等式得证.
4.证明 根据三角不等式,有$$LHS=\sqrt{\dfrac 34a^2+\left(b+\dfrac 12a\right)^2}+\sqrt{\dfrac 34a^2+\left(c+\dfrac 12a\right)^2}\geqslant \sqrt{\left(\dfrac{\sqrt 3}2a+\dfrac{\sqrt 3}2a\right)^2+\left(b+\dfrac 12a+c+\dfrac 12a\right)^2}=RHS,$$等号取得的条件为向量$\left(\dfrac{\sqrt 3}2a,b+\dfrac 12a\right)$与向量$\left(\dfrac{\sqrt 3}2a,c+\dfrac 12a\right)$同向,也即$$\begin{cases} a=0,\\bc\geqslant 0,\end{cases}\lor \begin{cases} a\neq 0,\\b-c=0.\end{cases} $$
5.证明 注意到取等条件为$a=b=1$,此时$$(a+b)^2=a^2+b^2+2ab\leqslant a^2+b^2+a^2b^2+1= (a^2+1)(b^2+1),$$且$$(ab+1)^2=a^2b^2+1+2ab\leqslant a^2b^2+1+a^2+b^2=(a^2+1)(b^2+1),$$因此$$\dfrac{b^2+2}{a+b}+\dfrac{a^2}{ab+1}\geqslant \dfrac{b^2+2+a^2}{\sqrt{(a^2+1)(b^2+1)}}=\dfrac{(a^2+1)+(b^2+1)}{\sqrt{(a^2+1)(b^2+1)}}\geqslant 2,$$等号$a=b=1$时取得.因此原命题得证.
注意到取等条件,利用不等式将分母“通分”,使得问题得到简化.
6.证明 令$a_0=1$,则在$\dfrac{a_{n+1}}{a_{n+2}}+\dfrac{a_n}{a_{n+2}}=1$中,分别令$n=1,2,\cdots $累加可得$$\left(\dfrac{a_1}{a_2}+\dfrac{a_2}{a_3}+\cdots +\dfrac{a_n}{a_{n+1}}\right)+\left(\dfrac{a_0}{a_2}+\dfrac{a_1}{a_3}+\cdots +\dfrac{a_{n-1}}{a_{n+1}}\right)=n,$$对两个括号分别应用均值不等式,可得$$n\geqslant n\cdot \left(\dfrac{a_1}{a_2}\cdot \dfrac{a_2}{a_3}\cdots\dfrac{a_n}{a_{n+1}}\right)^{\frac 1n}+n\cdot \left(\dfrac{a_0}{a_2}\cdot \dfrac{a_1}{a_3}\cdots \dfrac{a_{n-1}}{a_{n+1}}\right)^{\frac 1n}=n\cdot a_{n+1}^{-\frac 1n}+n\cdot a_n^{-\frac 1n}\cdot a_{n+1}^{-\frac 1n},$$整理即得.
7.解 看到分母$t^2+1$,联想到恒等式$\left(\dfrac{t^2-1}{t^2+1}\right)^2+\left(\dfrac{2t}{t^2+1}\right)^2=1$,以及三角换元.
法一(代数变形)
根据已知,有$$x-2y=\dfrac{t^2+4}{t^2+1}=1+\dfrac{3}{t^2+1},$$且$$2x-y=\dfrac{2t^2+2-3t}{t^2+1}=2-\dfrac{3t}{t^2+1},$$因此$$\begin{cases} x-2y-\dfrac 52=\dfrac 32\cdot \dfrac{1-t^2}{t^2+1},\\ 2x-y-2=-\dfrac 32\cdot \dfrac{2t}{t^2+1},\end{cases} $$于是该参数方程对应的普通方程为$$\left(x-2y-\dfrac 52\right)^2+(2x-y-2)^2=\dfrac 94,$$也即$$5x^2+5y^2-8xy-13x+14y+8=0.$$这是一个椭圆,对称中心$E$可由直线$x-2y-\dfrac 52=0$和直线$2x-y-2=0$联立解得为$E\left(\dfrac 12,-1\right)$,如图.
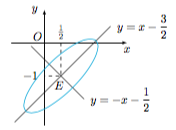 注意到这两条直线关于$y=x-\dfrac 32$和$y=-x-\dfrac 12$对称,即该椭圆的对称轴的方程.分别将直线$y=x-\dfrac 32$与$y=-x-\dfrac 12$与椭圆$E$联立可得$$2\left(x-\dfrac 12\right)^2=\dfrac 94,2\left(3x-\dfrac 32\right)^2=\dfrac 94,$$因此长轴长平方与短轴长平方之比为$9:1$,进而可得离心率为$\dfrac{2\sqrt 2}3$.
注意到这两条直线关于$y=x-\dfrac 32$和$y=-x-\dfrac 12$对称,即该椭圆的对称轴的方程.分别将直线$y=x-\dfrac 32$与$y=-x-\dfrac 12$与椭圆$E$联立可得$$2\left(x-\dfrac 12\right)^2=\dfrac 94,2\left(3x-\dfrac 32\right)^2=\dfrac 94,$$因此长轴长平方与短轴长平方之比为$9:1$,进而可得离心率为$\dfrac{2\sqrt 2}3$.
事实上,长轴长和短轴长分别为$3$和$1$.
思考与总结 抓住$t^2+1$的倍数进行加减,这样就能得到$\dfrac{1}{t^2+1}$和$\dfrac{t}{t^2+1}$,接下来朝恒等式靠拢即可.
法二(三角换元)
令$t=\tan \theta$,则$$x=\sin^2\theta-2\sin\theta\cos\theta=-\sin 2\theta-\dfrac 12\cos 2\theta+\dfrac 12,$$且$$y=-\sin\theta\cos\theta-2\cos^2\theta=-\dfrac 12\sin 2\theta-\cos 2\theta-1,$$从而解得$$\begin{cases} \sin 2\theta=-\dfrac 43x+\dfrac 23y+\dfrac 43,\\ \cos 2\theta =\dfrac 23x-\dfrac 43y-\dfrac 53,\end{cases} $$于是由$$\left(-\dfrac 43x+\dfrac 23y+\dfrac 43\right)^2+\left(\dfrac 23x-\dfrac 43y-\dfrac 53\right)^2=1$$化简即得,以下略.
注 下面就如何从方程$$\left(x-2y-\dfrac 52\right)^2+(2x-y-2)^2=\dfrac 94,$$得到椭圆的信息作一些说明.
首先,由二次曲线是有界曲线且不是圆知,曲线表示的是椭圆.
其次,联立直线$$\begin{cases} x-2y-\dfrac 52=0,\\2x-y-2=0,\end{cases}$$得到它们的交点$E\left(\dfrac 12,-1\right )$,这就是椭圆的中心(椭圆上的任意一点关于$E$的对称点在椭圆上).于是我们将坐标系的原点平移到点$E$,得到新坐标系$x'Ey'$,坐标变换公式为$$\begin{cases} x'=x-\dfrac 12,\\y'=y+1. \end{cases} $$于是得到曲线在新坐标系下的方程为$$(x'-2y')^2+(2x'-y')^2=\dfrac 94.$$这条曲线关于$y'=x'$以及$y'=-x'$对称,所以$y'=\pm x'$是椭圆的两条对称轴,即$y=x-\dfrac 32$与$y=-x-\dfrac 12$是椭圆的两条对称轴.
