已知三棱锥\(P-ABC\)底面是边长为\(2\)的等边三角形,若\(PA=PB=\sqrt 2\),二面角\(P-BA-C\)的大小为\(60^\circ\),则三棱锥\(P-ABC\)的外接球半径\(R=\)_______.
 正确答案是\(\dfrac{\sqrt{13}}{3}\).
正确答案是\(\dfrac{\sqrt{13}}{3}\).
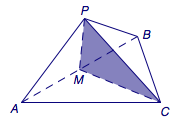
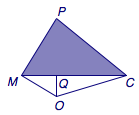
如图,设\(M\)为\(AB\)的中点,我们在平面\(PMC\)里研究外接球球心\(O\)的位置.
事实上,\(O\)在任何一个面的投影都是这个面的外心,于是\(O\)在底面\(ABC\)上投影的位置是其中心\(Q\),而在侧面\(PAB\)上投影的位置就是\(M\)(注意到三角形\(PAB\)为直角三角形,\(AB\)为斜边).
接下来的计算很容易,\(MQ=\dfrac{\sqrt 3}3\),而\(\angle OMQ=30^\circ\),因此\(OQ=\dfrac 13\).进而\[R=OC=\sqrt{OQ^2+QC^2}=\dfrac{\sqrt{13}}3.\]

倒数第二行,OH应为OQ