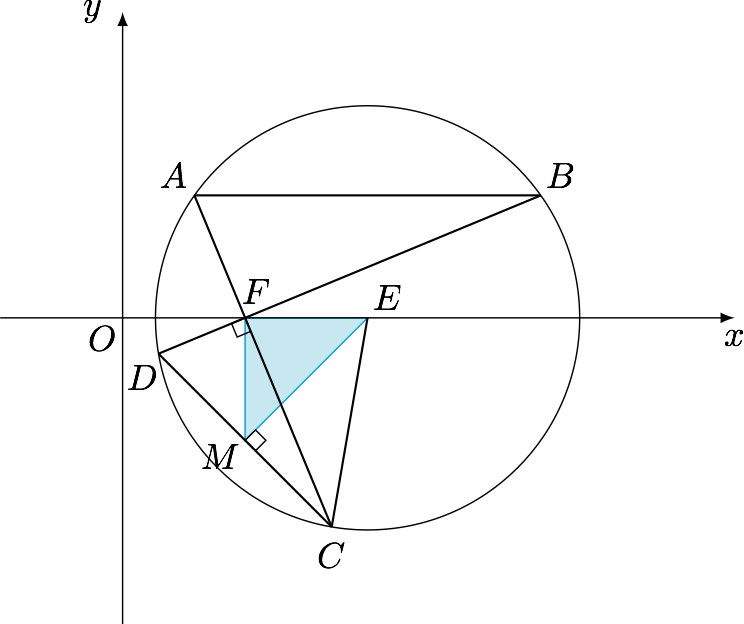
已知圆$E:(x-2)^2+y^2=3$,设直线$l_1:x-my-1=0$交圆$E$于$A,C$两点,直线$l_2:mx+y-m=0$交圆$E$于$B,D$两点.线段$AB,CD$分别位于$x$轴的上方和下方.当$CD$的斜率为$-1$时,求线段$AB$的长.
分析 注意到直线$l_1$与直线$l_2$是过$F(1,0)$且互相垂直的两条直线.在这样浓厚的几何色彩下,我们选择利用三角知识解决问题.
解 取$CD$的中点$M$,连接$FM,EM,EC$.由$CD$的斜率为$-1$可得$\angle FEM=45^\circ$,在$\triangle FEM$中应用余弦定理,有$$FM^2=FE^2+EM^2-2FE\cdot EM\cdot\cos 45^\circ,$$又$FM^2=EC^2-EM^2$,代入数据可得$$EM=\sqrt 2,FM=1,$$进而$FM\perp FE$,因此$\angle FMD=45^\circ$,于是$\angle FCD=22.5^\circ$,进而$$FC=2\cos 22.5^\circ,FD=2\sin 22.5^\circ.$$
根据圆幂定理,有$$DF\cdot FB=CF\cdot FA=EC^2-EF^2=2,$$从而\[\begin{split} AB^2&=AF^2+BF^2\\ &=\dfrac{1}{\sin^222.5^\circ}+\dfrac{1}{\cos^222.5^\circ}\\ &=\dfrac{4}{\sin^245^\circ} \\ &=8,\end{split} \]因此线段$AB$的长为$2\sqrt 2$.