每日一题[445]代数与几何

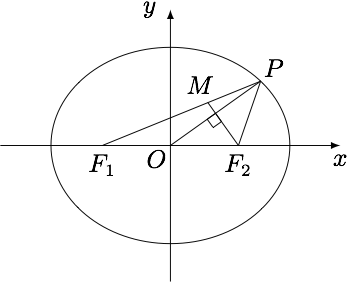
已知椭圆$E:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1$的左、右焦点分别为$F_1,F_2$．$P$是椭圆上一点，直线$F_2M$垂直于$OP$且交线段$F_1P$于点$M$，若$F_1M=2MP$，求椭圆$E$的离心率$e$的取值范围．

正确答案是$\left[\dfrac 12,1\right)$．

方法一    代数方程

设$F_1(-c,0)$，$F_2(c,0)$，$P(x,y)$，则$M\left(\dfrac 23x-\dfrac 13c,\dfrac 23y\right)$．由$MF_2\perp OP$可得 $$\dfrac yx\cdot \dfrac{\dfrac 23y}{\dfrac 23x-\dfrac 43c}=-1,$$ 整理得 $$x^2+y^2-2cx=0,$$ 将$y^2=b^2\cdot\left(1-\dfrac {x^2}{a^2}\right)$代入，可得 $$\dfrac{c^2}{a^2}x^2-2cx+b^2=0.$$ 该方程在$[-a,a]$上有根，又该方程的两根不等，且同正，两根之和大于$2a$，故它在$[-a,a]$上有且只有一根，因此 $$\dfrac{c^2}{a^2}\cdot a^2-2ca+b^2\leqslant 0,$$ 解得$e\geqslant \dfrac 12$，从而$e$的取值范围是$\left[\dfrac 12,1\right)$．

方法二    平面几何

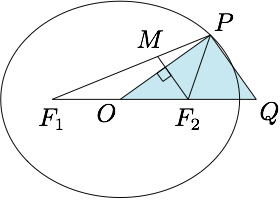
延长$OF_2$至$Q$，使得$F_2Q=F_2O$，连接$PQ$，则有$MF_2\parallel PQ$，于是$\angle OPQ$为直角，从而$PF_2=c$，其中$c$为椭圆$E$的半焦距．因此 $$a-c\leqslant c\leqslant a+c,$$ 解得$e\geqslant \dfrac 12$，进而$e$的取值范围是$\left[\dfrac 12,1\right)$．

注    利用平面向量知识，可以由$\overrightarrow{F_2M}\cdot \overrightarrow{OP}=0$得到 $$\left(\overrightarrow{OM}-\overrightarrow{OF_2}\right)\cdot \overrightarrow{OP}=0,$$ 即 $$\left(\dfrac 23\overrightarrow{OP}+\dfrac 13\overrightarrow{OF_1}-\overrightarrow{OF_2}\right)\cdot\overrightarrow{OP}=0,$$ 从而 $$\left(\overrightarrow{OP}-2\overrightarrow{OF_2}\right)\cdot \overrightarrow{OP}=0,$$ 这就提示我们倍长$OF_2$．